题目内容
△ABC三个顶点坐标分别为A(2,2)、B(4,2)、C(6,4),以原点O为位似中心,将△ABC缩小后得到的△DEF与△ABC对应边的比为1:2,这时△DEF各个顶点的坐标分别是多少?
考点:位似变换,坐标与图形性质
专题:
分析:根据相似比为1:2可得:A、B、C三点坐标分别乘以
或-
即可算出它的对应顶点的坐标.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵A(2,2)、B(4,2)、C(6,4),
∴以O点为位似中心,相似比为
,将△ABC缩小,则它的对应顶点的坐标是(1,1),(2,1),(3,2);
或(-1,-1),(-2,-1),(-3,-2);
∴以O点为位似中心,相似比为
| 1 |
| 2 |
或(-1,-1),(-2,-1),(-3,-2);
点评:此题主要考查了位似变换,以及坐标与图形的性质,关键是掌握若位似比是k,则原图形上的点(x,y),经过位似变化得到的对应点的坐标是(kx,ky)或(-kx,-ky).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
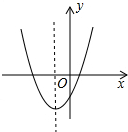 二次函数y=ax2+bx+c的图象如图,点(-
二次函数y=ax2+bx+c的图象如图,点(-| b |
| a |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,在Rt△ABC中,∠B=90°,AB=3cm,BC=4cm,点P从点A出发,以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.
如图,在Rt△ABC中,∠B=90°,AB=3cm,BC=4cm,点P从点A出发,以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.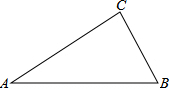 如图是一块直角三角形板材,其中,∠C=90°,AC=8cm,BC=6cm,请问:如何从这块板材上裁剪下一块面积最大的正方形?请画出你的设计图,并求出这块正方形的边长.
如图是一块直角三角形板材,其中,∠C=90°,AC=8cm,BC=6cm,请问:如何从这块板材上裁剪下一块面积最大的正方形?请画出你的设计图,并求出这块正方形的边长.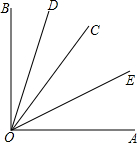 如图,∠AOB是直角,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数.
如图,∠AOB是直角,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数. 如图,已知直线AE、CD相交于点O,且∠AOB=90°,∠BOC=28°,求∠DOE、∠AOD的度数.
如图,已知直线AE、CD相交于点O,且∠AOB=90°,∠BOC=28°,求∠DOE、∠AOD的度数.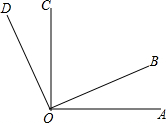 如图,∠AOD=120°,∠DOC=∠COB,∠AOC=75°.
如图,∠AOD=120°,∠DOC=∠COB,∠AOC=75°.