题目内容
化简:
+
+
.
| x-c |
| (x-a)(x-b) |
| b-c |
| (a-b)(x-b) |
| b-c |
| (b-a)(x-a) |
考点:分式的加减法
专题:
分析:根据加法结合律,可得
+[
+
],根据分式的性质,可化成同分母的分式,根据分式的加法,可得答案.
| x-c |
| (x-a)(x-b) |
| b-c |
| (a-b)(x-b) |
| b-c |
| (b-a)(x-a) |
解答:解:原式=
+[
+
]
=
+
=
+
=
-
=
=
=
.
| x-c |
| (x-a)(x-b) |
| b-c |
| (a-b)(x-b) |
| b-c |
| (b-a)(x-a) |
=
| x-c |
| (x-)(x-b) |
| (b-c)(x-a-x-b) |
| (x-a)(x-b)(a-b) |
=
| x-c |
| (x-a)(x-b) |
| (b-c)(b-a) |
| (x-a)(x-b)(a-b) |
=
| x-c |
| (x-a)(x-b) |
| b-c |
| (x-a)(x-b) |
=
| x-c-(b-c) |
| (x-a)(x-b) |
=
| x-b |
| (x-a)(x-b) |
=
| 1 |
| x-a |
点评:本题考查了分式的加减法,利用了加法结合律,先通分再加减运算.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
关于x的一元二次方程(a-1)x2-x+a2-1=0的一个根是0,则a的值为( )
| A、1或-1 | ||
| B、-1 | ||
| C、1 | ||
D、
|
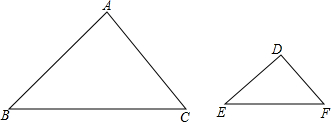 如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D.若△ABC的边BC上的高为6,面积为12
如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D.若△ABC的边BC上的高为6,面积为12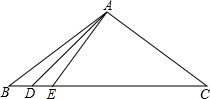 如图,△ABC中,D、E为BC边上的点,且AC⊥AD,∠BAD=∠DAE=12°,AB+AE=BC.求∠C的度数.
如图,△ABC中,D、E为BC边上的点,且AC⊥AD,∠BAD=∠DAE=12°,AB+AE=BC.求∠C的度数. 如图,在Rt△ABC中,∠B=90°,AB=3cm,BC=4cm,点P从点A出发,以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.
如图,在Rt△ABC中,∠B=90°,AB=3cm,BC=4cm,点P从点A出发,以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动. 如图,已知直线AE、CD相交于点O,且∠AOB=90°,∠BOC=28°,求∠DOE、∠AOD的度数.
如图,已知直线AE、CD相交于点O,且∠AOB=90°,∠BOC=28°,求∠DOE、∠AOD的度数.