题目内容
1.一条弦把圆分为2:3的两部分,那么这条弦所对较小的圆周角度数为72°.分析 先求出这条弦所对圆心角的度数,然后分情况讨论这条弦所对圆周角的度数,即可得出结论.
解答 解:如图,连接OA、OB.
弦AB将⊙O分为2:3两部分,
则∠AOB=$\frac{1}{2}$×360°=144°;
∴∠ACB=$\frac{1}{2}$∠AOB=72°,
∠ADB=180°-∠ACB=108°;
故这条弦所对较小的圆周角的度数为72°;
故答案为:72°.
点评 本题考查了圆周角定理以及圆内接四边形的性质;需注意的是在圆中,一条弦(非直径)所对的圆周角应该有两种情况.

练习册系列答案
相关题目
20.在下列各组中,哪个选项表示互为相反意义的是( )
| A. | 足球比赛胜5场与负6场 | B. | 向东走3千米,再向前走3千米 | ||
| C. | 增产10吨粮食与减产-10吨粮食 | D. | 下降的反义词是上升 |
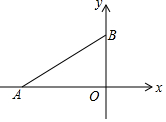 如图,在平面直角坐标系中,A,B两点的坐标分别为(-4,0),(0,3),连接AB.点P在第二象限,若以点P,A,B为顶点的三角形是等腰直角三角形,则点P坐标为(-$\frac{7}{2}$,$\frac{7}{2}$)或(-3,7)或(-7,4).
如图,在平面直角坐标系中,A,B两点的坐标分别为(-4,0),(0,3),连接AB.点P在第二象限,若以点P,A,B为顶点的三角形是等腰直角三角形,则点P坐标为(-$\frac{7}{2}$,$\frac{7}{2}$)或(-3,7)或(-7,4).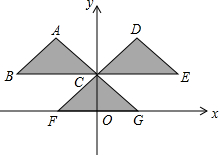 如图,三角形CFG的顶点坐标分别为C(0,$\frac{\sqrt{2}}{2}$),F(-$\frac{\sqrt{2}}{2}$,0),G($\frac{\sqrt{2}}{2}$,0).把三角形CFG平移两次,构成如图所示的图案(其中点B、C、E在一条平行于x轴的直线上).
如图,三角形CFG的顶点坐标分别为C(0,$\frac{\sqrt{2}}{2}$),F(-$\frac{\sqrt{2}}{2}$,0),G($\frac{\sqrt{2}}{2}$,0).把三角形CFG平移两次,构成如图所示的图案(其中点B、C、E在一条平行于x轴的直线上).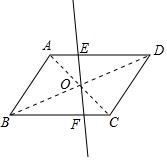 观察发现:直线l在绕点O旋转的过程中,①以E、F为端点的线段中,哪些线段的长度发生了变化?
观察发现:直线l在绕点O旋转的过程中,①以E、F为端点的线段中,哪些线段的长度发生了变化?