题目内容
12．求函数y=2（x-1）（x+2）图象的对称轴以及图象与x轴的交点坐标．分析 令y=0代入函数解析式中即可求出函数与x轴的两个交点坐标，由于抛物线的图象是对称的，所以根据抛物线与x轴的两交点即可求出对称轴．
解答 解：令y=0代入y=2（x-1）（x+2），
∴x=1或x=-2
∴y=2（x-1）（x+2）与x轴的两个交点为（1，0）和（-2，0）
∴对称轴方程为x=$\frac{-2+1}{2}$=-$\frac{1}{2}$
点评 本题考查抛物线与x轴的交点，解题的关键是令y=0代入抛物线的解析式中即可求出抛物线与x轴的两个交点，从而求出对称轴，本题属于基础题型．
练习册系列答案
相关题目
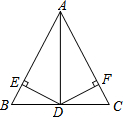如图，在△ABC中，AB=AC，AD平分∠BAC，交BC于点D，DE⊥AB于点E，DF⊥AC于点F，对于下列结论：①AD⊥BC；②AE=AF；③AD上任意一点到AB，AC的距离相等；④AD上任意一点到点B，点C的距离相等．其中正确结论的个数是（ ）
3．己知△ABC中，∠C=Rt∠，若AC=$\sqrt{3}$，BC=1，则sinA的值是（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{3}$ |
如图，把△ABC平移，使点A平移到点O．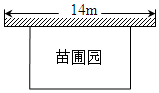
某中学课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边周长为30米的篱笆围成．已知墙长为14米（如图所示），设这个苗圃园垂直于墙的一边长为x米．