题目内容
11．已知关于x、y的方程组$\left\{\begin{array}{l}{3x+5y=m+2}\\{2x+3y=m}\end{array}\right.$，其中x与y的和为2，求m的值．分析 把原方程组消去m后，与x+y=2建立新的方程组，求得x，y的值后，再代入原方程组中，求得m的值．
解答 解：关于x、y的方程组为：$\left\{\begin{array}{l}{3x+5y=m+2①}\\{2x+3y=m②}\end{array}\right.$，
由①-②得：x+2y=2，
∵x、y的值之和等于2，
∴$\left\{\begin{array}{l}{x+2y=2}\\{x+y=2}\end{array}\right.$，
解这个方程组得$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$，
把$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$代入②得：m=4．
点评 本题考查的是解二元一次方程组，熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
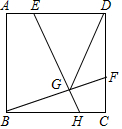如图，正方形ABCD中，点E在边AD上，点F在边CD上，AE=CF，EH⊥BF于点G，连接DG．
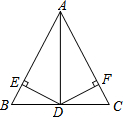如图，在△ABC中，AB=AC，AD平分∠BAC，交BC于点D，DE⊥AB于点E，DF⊥AC于点F，对于下列结论：①AD⊥BC；②AE=AF；③AD上任意一点到AB，AC的距离相等；④AD上任意一点到点B，点C的距离相等．其中正确结论的个数是（ ）
19．将函数y=$\frac{1}{2}$x2-x化为y=a（x-m）2+k的形式，得（ ）
| A． | y=$\frac{1}{2}$（x-1）2-$\frac{1}{2}$ | B． | y=$\frac{1}{2}$（x-$\frac{1}{4}$）2+$\frac{1}{32}$ | C． | y=$\frac{1}{2}$（x-1）2+$\frac{1}{2}$ | D． | y=$\frac{1}{2}$（x-$\frac{1}{4}$）2-$\frac{1}{32}$ |
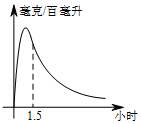实验数据显示：一般成人喝半斤低度白酒后，1.5小时内（包括1.5小时）其血液中酒精含量y（毫克/百毫升）与时间x（时）的关系可近似地用二次函数y=-200x2+400x表示，1.5小时后（包括1.5小时）y与x可近似地用反比例函数y=$\frac{k}{x}$（k＞0）表示（如图所示）
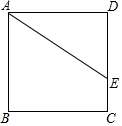已知正方形ABCD中，点E在边DC上，DE=3，EC=1，如图所示，把线段AE绕点A旋转，使点E落在直线BC上的点F处，则F、C两点的距离为1或7．
3．己知△ABC中，∠C=Rt∠，若AC=$\sqrt{3}$，BC=1，则sinA的值是（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{3}$ |
如图，把△ABC平移，使点A平移到点O．