题目内容
15.关于x的一元二次方程(x-2)(x-3)=m有两个不相等的实数根x1,x2,求m的取值范围;若x1,x2满足等式x1x2-x1-x2+1=0,求m的值.分析 原方程可化为x2-5x+6-m=0,于是得到△=b2-4ac=25-24+4m=1+4m,根据方程(x-2)(x-3)=m有两个不相等的实数根,得到△>0,求得m>-$\frac{1}{4}$根据根与系数的关系得到x1+x2=5,x1x2=6-m解方程即可得到结论.
解答 解:原方程可化为x2-5x+6-m=0,
△=b2-4ac=25-24+4m=1+4m,
∵方程(x-2)(x-3)=m有两个不相等的实数根,
∴△>0,
∴1+4m>0,
∴m>-$\frac{1}{4}$
∵x1+x2=5,x1x2=6-m
∴5-6+m+1=0,
∴m=0.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
20.下列四个实数中是无理数是( )
| A. | 0 | B. | π | C. | $\frac{22}{7}$ | D. | $\sqrt{16}$ |
4.在Rt△ABC中,∠C=90°,AC=6,BC=8,则以点C为圆心,半径为4.8的圆C与AB的位置关系是( )
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 不确定 |
5.一元二次方程x2-x-2=0的解是( )
| A. | x1=-1,x2=-2 | B. | x1=1,x2=-2 | C. | x1=1,x2=2 | D. | x1=-1,x2=2 |
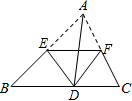 在三角形纸片ABC中.点E为AB边中点,将△ABC沿过点E的直线折叠,折痕交AC于F,并使点A与落在BC边上的点D.求证:点F平分AC.
在三角形纸片ABC中.点E为AB边中点,将△ABC沿过点E的直线折叠,折痕交AC于F,并使点A与落在BC边上的点D.求证:点F平分AC.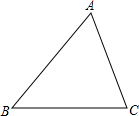 如图,已知锐角三角形ABC.
如图,已知锐角三角形ABC.