题目内容
5.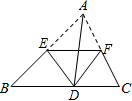 在三角形纸片ABC中.点E为AB边中点,将△ABC沿过点E的直线折叠,折痕交AC于F,并使点A与落在BC边上的点D.求证:点F平分AC.
在三角形纸片ABC中.点E为AB边中点,将△ABC沿过点E的直线折叠,折痕交AC于F,并使点A与落在BC边上的点D.求证:点F平分AC.
分析 根据折叠的性质得到DA=DF,AE=FE,∠ADE=∠FDE,根据等腰三角形性质得∠B=∠DFB,再根据三角形外角性质得到∠ADE+∠FDE=∠B+∠DFB,则∠ADE=∠B,所以DE∥BC,易得DE为△ABC的中位线,得到AE=EC,于是EF=EC.
解答 证明:∵将△ABC沿过点E的直线折叠,折痕交AC于F,并使点A与落在BC边上的点D,
∴DA=DF,AE=FE,∠ADE=∠FDE,
∴∠B=∠DFB,
∵∠ADF=∠B+∠DFB,即∠ADE+∠FDE=∠B+∠DFB,
∴∠ADE=∠B,
∴DE∥BC,
∵D为AB的中点,
∴DE为△ABC的中位线,
∴AE=EC,
∴EF=EC,
即点F平分AC.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了三角形中位线性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.在比例尺是1:46000的城市交通游览图上,某条道路的图上距离长约8cm,则这条道路的实际长度约为( )
| A. | 368×103cm | B. | 36.8×104cm | C. | 3.68×105cm | D. | 3.68×106cm |
10.下列艺术字是轴对称图形的是( )
| A. | 理 | B. | 想 | C. | 高 | D. | 中 |
7.绝对值等于2的数是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 0或2 |
14.下列语句中,正确的个数是( )
①平面上,一条直线只有一条垂线;
②过直线上一点,画已知直线的垂线只能画一条;
③过直线外一点且垂直于这条直线的垂线有且只有一条;
④过一点有且只有一条直线与已知直线垂直.
①平面上,一条直线只有一条垂线;
②过直线上一点,画已知直线的垂线只能画一条;
③过直线外一点且垂直于这条直线的垂线有且只有一条;
④过一点有且只有一条直线与已知直线垂直.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.一个直角三角形的三边分别是6cm、8cm、xcm,则x=( )cm.
| A. | 100cm | B. | 10cm | C. | 10cm或2$\sqrt{7}$cm | D. | 100cm或28cm |