题目内容
4.在Rt△ABC中,∠C=90°,AC=6,BC=8,则以点C为圆心,半径为4.8的圆C与AB的位置关系是( )| A. | 相切 | B. | 相交 | C. | 相离 | D. | 不确定 |
分析 先根据题意画出图形,再结合切线的性质及勾股定理、三角形的面积公式解答即可.
解答 解:设以C为圆心的圆与AB相切于点D,
根据切线的性质知,CD是圆C的半径,也是直角三角形斜边上的高,
由勾股定理知,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,S△ABC=$\frac{1}{2}$AC•AB=$\frac{1}{2}$AB•CD,
∴CD=4.8,
∵r=4.8,
∴d=r,
即半径为4.8的圆C与AB的位置关系是相切,
故选A.
点评 本题考查了直线和圆的位置关系,解题的关键是判断圆的半径和圆心到直线的距离.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
13.下列事件中,属于随机事件的是( )
| A. | 袋中只有5个黄球,摸出一个球是白球 | |
| B. | 从分别写有2,4,6的三张卡片中随机抽出一张,卡片上的数字能被2整除 | |
| C. | 用长度分别是2cm,3cm,6cm的细木条首尾相连组成一个三角形 | |
| D. | 任意买一张电影票,座位号是偶数 |
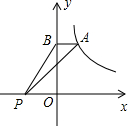 如图,A是反比例函数图象上的一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为4,则这个反比例函数的关系式为y=$\frac{8}{x}$.
如图,A是反比例函数图象上的一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为4,则这个反比例函数的关系式为y=$\frac{8}{x}$.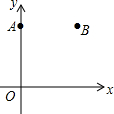 如图,在平面直角坐标系xOy中,已知点A(0,6),点B(6,6).
如图,在平面直角坐标系xOy中,已知点A(0,6),点B(6,6). 如图,AB和DE是直立在地面上的两根立柱,已知AB=5m,某一时刻AB在太阳光下的影子长BC=3m.
如图,AB和DE是直立在地面上的两根立柱,已知AB=5m,某一时刻AB在太阳光下的影子长BC=3m.