题目内容
7.先化简,再求值:2a-$\sqrt{{a}^{2}-4a+4}$,其中a=$\sqrt{3}$.小刚的解法如下:2a-$\sqrt{{a}^{2}-4a+4}$=2a-$\sqrt{(a-2)^2}$=2a-(a-2)=2a-a+2=a+2,当a=$\sqrt{3}$时,2a-$\sqrt{{a}^{2}-4a+4}$=$\sqrt{3}$+2.小刚的解法对吗?若不对,请改正.分析 根据二次根式的性质得到原式=2a-$\sqrt{(a-2)^2}$=2a-|a-2|,由于a=$\sqrt{3}$,即a-2<0,则原式=2a+a-2=3a-2,然后把a的值代入计算.
解答 解:不对.
2a-$\sqrt{{a}^{2}-4a+4}$
=2a-$\sqrt{(a-2)^2}$
=2a-|a-2|,
当a=$\sqrt{3}$时,a-2<0,原式=2a+a-2=3a-2=3$\sqrt{3}$-2.
点评 本题考查了二次根式的化简求值:先根据二次根式的性质和已知条件把所求的式子进行化简,然后把满足条件的字母的值代入计算.

练习册系列答案
相关题目
15.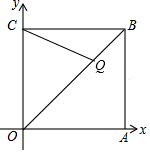 如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A、C分别在x轴、y轴的正半轴上,点Q在对角线OB上,若OQ=OC,则点Q的坐标为($\sqrt{2}$,$\sqrt{2}$).
如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A、C分别在x轴、y轴的正半轴上,点Q在对角线OB上,若OQ=OC,则点Q的坐标为($\sqrt{2}$,$\sqrt{2}$).
 如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A、C分别在x轴、y轴的正半轴上,点Q在对角线OB上,若OQ=OC,则点Q的坐标为($\sqrt{2}$,$\sqrt{2}$).
如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A、C分别在x轴、y轴的正半轴上,点Q在对角线OB上,若OQ=OC,则点Q的坐标为($\sqrt{2}$,$\sqrt{2}$).
19. 如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字( )
如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字( )
 如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字( )
如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字( )| A. | 的 | B. | 中 | C. | 国 | D. | 梦 |
16.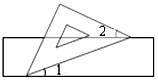 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=25°,那么∠1的度数是( )
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=25°,那么∠1的度数是( )
 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=25°,那么∠1的度数是( )
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=25°,那么∠1的度数是( )| A. | 20o | B. | 25o | C. | 30o | D. | 15o |
17.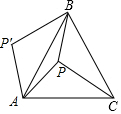 P为△ABC内一点,且PA=4,PC=5,PB=3,将△APC绕点A逆时针旋转使P与P’对应,C与B对应,则四边形AP′BP的面积为( )
P为△ABC内一点,且PA=4,PC=5,PB=3,将△APC绕点A逆时针旋转使P与P’对应,C与B对应,则四边形AP′BP的面积为( )
 P为△ABC内一点,且PA=4,PC=5,PB=3,将△APC绕点A逆时针旋转使P与P’对应,C与B对应,则四边形AP′BP的面积为( )
P为△ABC内一点,且PA=4,PC=5,PB=3,将△APC绕点A逆时针旋转使P与P’对应,C与B对应,则四边形AP′BP的面积为( )| A. | 4$\sqrt{3}$+6 | B. | 12$\sqrt{3}$+6 | C. | 60 | D. | 42 |
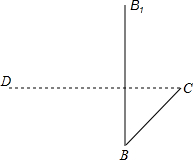 (1)用斜二测画法补全长方体ABCD-A1B1C1D1 (不必写画法);
(1)用斜二测画法补全长方体ABCD-A1B1C1D1 (不必写画法);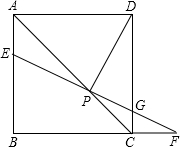 已知:如图,点P是正方形ABCD的对角线AC上一点,过点P作EF⊥DP,交AB于点E,交CD于点G,交BC的延长线于点F.
已知:如图,点P是正方形ABCD的对角线AC上一点,过点P作EF⊥DP,交AB于点E,交CD于点G,交BC的延长线于点F.