题目内容
12.如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O.
(1)求证:OB=OC;
(2)若∠ABC=55°,求∠BOC的度数.
分析 (1)由AB=AC,利用等边对等角得到一对角相等,再由垂直的定义得到一对直角相等,利用ASA得到三角形BOE与三角形COD全等,利用全等三角形对应边相等即可得证;
(2)由底角的度数,利用等腰三角形性质求出顶角度数,利用四边形内角和定理得到∠A与∠DOE互补,求出∠DOE度数即为所求.
解答 (1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BD、CE是△ABC的两条高线,
∴∠BEC=∠BDC=90°,
∴△BEC≌△CDB,
∴∠DBC=∠ECB,BE=CD.
在△BOE和△COD中,
$\left\{\begin{array}{l}{∠BOE=∠COD}\\{BE=CD}\\{∠BEC=∠BDE=90°}\end{array}\right.$,
∴△BOE≌△COD,
∴OB=OC;
(2)解:∵∠ABC=55°,AB=AC,
∴∠A=180°-2×55°=70°,
∵∠DOE+∠A=180°,
∴∠BOC=∠DOE=180°-70°=110°.
点评 此题考查了全等三角形的判定与性质,等腰三角形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
2.泉州市某校准备组织教师、学生、家长到福州进行参观学习活动,旅行社代办购买动车票,动车票价格如表所示:
根据报名总人数,若所有人员都买一等座的动车票,则共需13650元;若都买二等座动车票,则共需8820元.已知家长人数是教师人数的2倍.
(1)设参加活动的老师有m人,请直接用含m的代数式表示:教师和家长都购买一等动车票所需的总费用;
(2)求参加活动的教师、家长、学生各有多少人?
(3)如果二等座动车票共买到x张,其中学生全部购买二等座动车票,剩余的人员买一等座动车票,且买票的总费用不低于9000元,求x的最大值.
| 运行区间 | 大人票价 | 学生票价 | |||
| 出发站 | 终点站 | 一等座 | 二等座 | 一等座 | 二等座 |
| 泉州 | 福州 | 65(元) | 54(元) | 65(元) | 40(元) |
(1)设参加活动的老师有m人,请直接用含m的代数式表示:教师和家长都购买一等动车票所需的总费用;
(2)求参加活动的教师、家长、学生各有多少人?
(3)如果二等座动车票共买到x张,其中学生全部购买二等座动车票,剩余的人员买一等座动车票,且买票的总费用不低于9000元,求x的最大值.
17.在平面直角坐标系中,若点P(a,b)在第二象限,则点Q(2-a,-1-b)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.如图是若干个相同的小正方体组成的一个几何体的三视图,则小正方体的个数是( )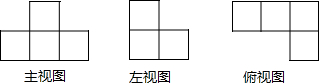

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
1.当x=-1时,代数式-x2-2x+1的值是( )
| A. | -2 | B. | 2 | C. | -1 | D. | 4 |
 如图,C是线段AB上的一点,M是AC的中点,N是BC的中点,若AB=6,则MN的长为3.
如图,C是线段AB上的一点,M是AC的中点,N是BC的中点,若AB=6,则MN的长为3. 如图,∠ABC=∠DBE=90°,AB=DB,∠A=∠D=30°,点E在AC上,△ABC绕点B顺时针旋转,当点C落在DE上时,旋转角为60度.
如图,∠ABC=∠DBE=90°,AB=DB,∠A=∠D=30°,点E在AC上,△ABC绕点B顺时针旋转,当点C落在DE上时,旋转角为60度.