题目内容
14.如果实数x,y满足y=$\frac{1}{3}$x-1,那么$\frac{1}{3}$x2-2xy+3y2-2的值为1.分析 由y=$\frac{1}{3}$x-1,得出x-3y=3,再进一步利用提取公因式法和完全平方公式因式分解,整体代入求得答案即可.
解答 解:∵y=$\frac{1}{3}$x-1,
∴x-3y=3,
∴$\frac{1}{3}$x2-2xy+3y2-2
=$\frac{1}{3}$(x2-6xy+9y2)-2
=$\frac{1}{3}$(x-3y)2-2
=3-2
=1.
故答案为:1.
点评 此题考查因式分解的实际运用,利用提取公因式法和完全平方公式因式分解,整体代入是解决问题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
5.如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是( )
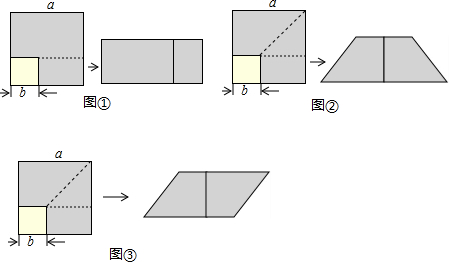

| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
2.不等式组$\left\{\begin{array}{l}{3x-1≥5}\\{2x+4<x+7}\end{array}\right.$的解集为( )
| A. | x≥2 | B. | x<3 | C. | 2≤x<3 | D. | x>3 |
19.-2015的绝对值是( )
| A. | -2015 | B. | 2015 | C. | $\frac{1}{2015}$ | D. | -$\frac{1}{2015}$ |
 (1)已知:如图,点C在线段AB上,AC=6,BC=4,点M、N分别是AC、BC的中点,求MN的长;
(1)已知:如图,点C在线段AB上,AC=6,BC=4,点M、N分别是AC、BC的中点,求MN的长; 如图,在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,BE∥DF,AD∥BC.求证:AD=BC.
如图,在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,BE∥DF,AD∥BC.求证:AD=BC.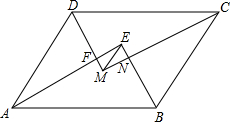 如图,?ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点N,连接EM.若?ABCD的周长为42cm,FM=6cm,EF=8cm,则EM=10cm,AB=15.5cm.
如图,?ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点N,连接EM.若?ABCD的周长为42cm,FM=6cm,EF=8cm,则EM=10cm,AB=15.5cm.