题目内容
13. 如图所示,直线AF分别截BD、CE于G、H,点B在AC上,若∠1=∠2,∠C=∠D,则DF与AC平行吗?为什么?
如图所示,直线AF分别截BD、CE于G、H,点B在AC上,若∠1=∠2,∠C=∠D,则DF与AC平行吗?为什么?
分析 先由对顶角相等,得到:∠1=∠DGF,然后根据等量代换得到:∠2=∠DGF,然后根据同位角相等两直线平行,得到BD∥CE,然后根据两直线平行,同位角相等,得到∠C=∠DBA,然后根据等量代换得到:∠D=∠DBA,最后根据内错角相等两直线平行,即可得到DF与AC平行.
解答 解:DF与AC平行.
理由:∵∠1=∠DGF,∠1=∠2,
∴∠2=∠DGF,
∴BD∥CE,
∴∠C=∠DBA,
∵∠C=∠D,
∴∠D=∠DBA,
∴DF∥AC.
点评 本题考查了平行线的性质和判定的应用,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然,题目比较好,难度适中.

练习册系列答案
相关题目
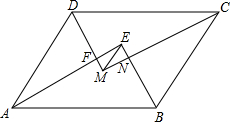 如图,?ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点N,连接EM.若?ABCD的周长为42cm,FM=6cm,EF=8cm,则EM=10cm,AB=15.5cm.
如图,?ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点N,连接EM.若?ABCD的周长为42cm,FM=6cm,EF=8cm,则EM=10cm,AB=15.5cm.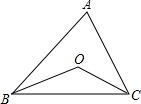 如图,△ABC的内角∠ABC,∠ACB的平分线相交于点O,∠A=n°,求∠BOC的度数.
如图,△ABC的内角∠ABC,∠ACB的平分线相交于点O,∠A=n°,求∠BOC的度数.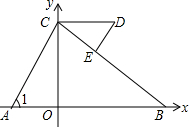 如图,平面直角坐标系中,C(0,5)、D(a,5)(a>0),A、B在x轴上,∠1=∠D,请写出∠ACB和∠BED数量关系以及证明.
如图,平面直角坐标系中,C(0,5)、D(a,5)(a>0),A、B在x轴上,∠1=∠D,请写出∠ACB和∠BED数量关系以及证明.