题目内容
3.解方程组$\left\{\begin{array}{l}{2x+y-z=0}\\{x-y+3z=12}\\{3x+2y-z=1}\end{array}\right.$.分析 加减消元法求解可得.
解答 解:$\left\{\begin{array}{l}{2x+y-z=0}&{①}\\{x-y+3z=12}&{②}\\{3x+2y-z=1}&{③}\end{array}\right.$,
①+②,得:3x+2z=12 ④,
①×2-③,得:x-z=-1 ⑤,
④+⑤×2,得:5x=10,解得:x=2,
将x=2代入⑤,得:2-z=-1,解得:z=3,
将x=2、z=3代入①,得:4+y-3=0,解得:y=-1,
∴方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\\{z=3}\end{array}\right.$.
点评 本题主要考查解三元一次方程组,熟练掌握加减消元法的步骤和依据是解题的关键.

练习册系列答案
相关题目
11.单项式-$\frac{3{a}^{2}b}{5}$的系数和次数分别是( )
| A. | $\frac{3}{5}$和2 | B. | $\frac{3}{5}$和3 | C. | -$\frac{3}{5}$和2 | D. | -$\frac{3}{5}$和3 |
8. 如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为( )
如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为( )
 如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为( )
如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为( )| A. | (0,0),2 | B. | (2,2),$\frac{1}{2}$ | C. | (2,2),2 | D. | (1,1),$\frac{1}{2}$ |
15.下列哪个是一元二次方程x2-6x+8=0的解( )
| A. | -2或-4 | B. | 2 | C. | 2或4 | D. | 无解 |
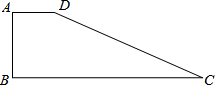 如图在四边形ABCD中,∠A=90°,AD=6,AB=8,BC=26,CD=24.
如图在四边形ABCD中,∠A=90°,AD=6,AB=8,BC=26,CD=24.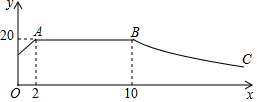 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且大棚内温度为20℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后大棚内温度y(单位:℃)随光照时间x(单位:h)变化的大致图象,其中BC段是双曲线y=$\frac{k}{x}$的一部分.请根据图中信息解答下列问题:
我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且大棚内温度为20℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后大棚内温度y(单位:℃)随光照时间x(单位:h)变化的大致图象,其中BC段是双曲线y=$\frac{k}{x}$的一部分.请根据图中信息解答下列问题: