题目内容
12.已知C,D两点在线段AB的垂直平分线上,且∠ACB=40°,∠ADB=68°,则∠CAD=126°或14°.分析 ①根据线段的垂直平分线的性质得到CA=CB,DA=DB,证明△CAD≌△CBD,得到答案;
②根据线段的垂直平分线的性质和等腰三角形的性质证明结论.
解答 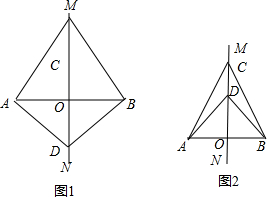 解:①如图1,∵点C、D为线段AB的垂直平分线上的两点,
解:①如图1,∵点C、D为线段AB的垂直平分线上的两点,
∴CA=CB,DA=DB,
在△CAD和△CBD中,
$\left\{\begin{array}{l}{CA=CB}\\{DA=DB}\\{CD=CD}\end{array}\right.$,
∴△CAD≌△CBD,
∴∠CAD=∠CBD,
∵∠ACB=40°,∠ADB=68°,
∴∠CAD=$\frac{1}{2}$(360°-40°-68°)=126°;
②如图2,∵点C为线段AB的垂直平分线上的点,
∴CA=CB,∴∠CAB=∠CBA=$\frac{1}{2}$(180°-40°)=70°,
∵点D为线段AB的垂直平分线上的点,
∴DA=DB,
∴∠DAB=∠DBA=$\frac{1}{2}$(180°-68°)=56°,
∴∠CAD=∠CBD=70°-56°=14°.
综上所述:∠CAD=126°或14°.
故答案为:126°或14°.
点评 此题主要考查线段的垂直平分线的性质,全等三角形的判定和性质,等腰三角形的性质,熟练掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
3.下列各式 $\frac{a}{2}$、$\frac{n}{2m}$、$\frac{1}{2π}$、$\frac{a}{b}$+1、$\frac{a+b}{3}$中分式有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
7.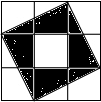 小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是( )
小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是( )
 小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是( )
小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
2.-3×(-2)=( )
| A. | $\frac{1}{6}$ | B. | 6 | C. | -6 | D. | $-\frac{1}{6}$ |
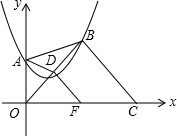 如图,抛物线y=a(x-1)2+$\sqrt{2}$(a≠0)经过y轴正半轴上的点A,点B,C分别是此抛物线和x轴上的动点,点D在OB上,且AD平分△ABO的面积,过D作DF∥BC交x轴于F点,则DF的最小值为$\frac{\sqrt{2}}{2}$.
如图,抛物线y=a(x-1)2+$\sqrt{2}$(a≠0)经过y轴正半轴上的点A,点B,C分别是此抛物线和x轴上的动点,点D在OB上,且AD平分△ABO的面积,过D作DF∥BC交x轴于F点,则DF的最小值为$\frac{\sqrt{2}}{2}$.
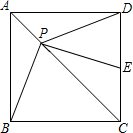 如图,边长为1的正方形ABCD中,P为对角线AC上的任意一点,分别连接PB、PD,
如图,边长为1的正方形ABCD中,P为对角线AC上的任意一点,分别连接PB、PD,