题目内容
6. 在Rt△ABC中,∠C=90°,AB=8,cosA=$\frac{3}{4}$,求∠B的三个三角函数值.
在Rt△ABC中,∠C=90°,AB=8,cosA=$\frac{3}{4}$,求∠B的三个三角函数值.
分析 根据一个角正弦等于它余角的余弦,正切的函数等于正弦比余弦,可得答案.
解答 解:∵ 在Rt△ABC中,∠C=90°,
在Rt△ABC中,∠C=90°,
∴∠A+∠B=90°,
∴sin∠B=cosA=$\frac{3}{4}$,
cos∠B=$\sqrt{1-co{s}^{2}∠B}$=$\frac{\sqrt{7}}{4}$,
tan∠B=$\frac{sin∠B}{cos∠B}$=$\frac{3\sqrt{7}}{7}$.
点评 本题考查了解直角三角形,互为余角的三角函数的关系,利用了互为余角的三角函数的关系.

练习册系列答案
相关题目
17.如果x=2是关于x的方程x-3=a-x的解,则a的值是( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
18.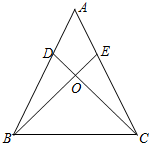 如图,在△ABC中,已知点D、E分别在AB、AC上,BE与CD相交于点O,依据下列各个选项中所列举的条件,不能说明AB=AC的是( )
如图,在△ABC中,已知点D、E分别在AB、AC上,BE与CD相交于点O,依据下列各个选项中所列举的条件,不能说明AB=AC的是( )
 如图,在△ABC中,已知点D、E分别在AB、AC上,BE与CD相交于点O,依据下列各个选项中所列举的条件,不能说明AB=AC的是( )
如图,在△ABC中,已知点D、E分别在AB、AC上,BE与CD相交于点O,依据下列各个选项中所列举的条件,不能说明AB=AC的是( )| A. | BE=CD,∠EBC=∠DCB | B. | AD=AE,BE=CD | C. | OD=OE,∠ABE=∠ACD | D. | BE=CD,BD=CE |
16.下列说法中,错误的是( )
| A. | 4的算术平方根是2 | B. | $\sqrt{81}$的平方根是±3 | ||
| C. | 121的平方根是±11 | D. | -1的平方根是±1 |