题目内容
18.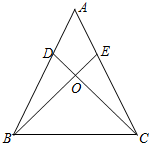 如图,在△ABC中,已知点D、E分别在AB、AC上,BE与CD相交于点O,依据下列各个选项中所列举的条件,不能说明AB=AC的是( )
如图,在△ABC中,已知点D、E分别在AB、AC上,BE与CD相交于点O,依据下列各个选项中所列举的条件,不能说明AB=AC的是( )| A. | BE=CD,∠EBC=∠DCB | B. | AD=AE,BE=CD | C. | OD=OE,∠ABE=∠ACD | D. | BE=CD,BD=CE |
分析 只要能确定AB、AC所在的两个三角形全等即可得出AB=AC,结合全等三角形的判定方法逐项判断即可.
解答 解:
当BE=CD,∠EBC=∠DCB时,结合∠A=∠A,在△ABE和△ACD中,利用“AAS”可证明△ABE≌△ACD,则有AB=AC,故A能得到AB=AC;
当AD=AE,BE=CD时,结合∠A=∠A,在△ABE和△ACD中,满足的是“ASS”无法证明△ABE≌△ACD,故B能得到AB=AC;
当OD=OE,∠ABE=∠ACD,结合∠BOD=∠COE,
在△BOD和△COE中,利用“AAS”可证明△BOD≌△COE,
∴OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴AB=AC,故C能得到AB=AC;
当BE=CD,BD=CE时,结合BC=CB,可证明△BCD≌△CBE,可得∠ABC=∠ACB,可得AB=AC,故D能得到AB=AC,
故选B.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
相关题目
9.在-2,0,-4,π这四个数中,最小的数是( )
| A. | -2 | B. | 0 | C. | -4 | D. | π |
 在Rt△ABC中,∠C=90°,AB=8,cosA=$\frac{3}{4}$,求∠B的三个三角函数值.
在Rt△ABC中,∠C=90°,AB=8,cosA=$\frac{3}{4}$,求∠B的三个三角函数值.