题目内容
6.计算题(1)$\frac{4{x}^{2}}{2x-3}$+$\frac{9}{3-2x}$
(2)$\frac{12}{{m}^{2}-9}$-$\frac{2}{m-3}$
(3)(-1)2+($\frac{1}{2}$)-4-5÷(2005-π)0
(4)1-$\frac{x-y}{x+2y}$÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}+4xy+4{y}^{2}}$
(5)$\frac{{a}^{2}}{a-b}$-a-b.
分析 (1)原式变形后,利用同分母分式的减法法则计算即可得到结果;
(2)原式通分并利用同分母分式的减法法则计算即可得到结果;
(3)原式利用零指数幂、负整数指数幂法则,以及乘方的意义计算即可得到结果;
(4)原式第二项利用除法法则变形,约分后通分并利用同分母分式的减法法则计算即可得到结果;
(5)原式通分并利用同分母分式的减法法则计算即可得到结果.
解答 解:(1)原式=$\frac{4{x}^{2}-9}{2x-3}$=$\frac{(2x+3)(2x-3)}{2x-3}$=2x+3;
(2)原式=$\frac{12-2(m+3)}{(m+3)(m-3)}$=$\frac{-2(m-3)}{(m+3)(m-3)}$=-$\frac{2}{m+3}$;
(3)原式=1+16-5=12;
(4)原式=1-$\frac{x-y}{x+2y}$•$\frac{(x+2y)^{2}}{(x+y)(x-y)}$=1-$\frac{x+2y}{x+y}$=$\frac{x+y-x-2y}{x+y}$=-$\frac{y}{x+y}$;
(5)原式=$\frac{{a}^{2}-(a+b)(a-b)}{a-b}$=$\frac{{b}^{2}}{a-b}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
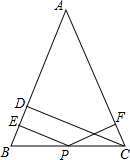 如图,在△ABC中,AB=AC,CD⊥AB于D,P为BC上的任意一点,过P点分别作PE⊥AB,PF⊥CA,垂足分别为E,F,则有PE+PF=CD,你能说明为什么吗?
如图,在△ABC中,AB=AC,CD⊥AB于D,P为BC上的任意一点,过P点分别作PE⊥AB,PF⊥CA,垂足分别为E,F,则有PE+PF=CD,你能说明为什么吗?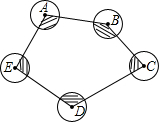 如图,五个半径为2的圆,圆心分别是点A,B,C,D,E,则图中阴影部分的面积和是多少?(S扇形=$\frac{nπR^2}{360°}$)
如图,五个半径为2的圆,圆心分别是点A,B,C,D,E,则图中阴影部分的面积和是多少?(S扇形=$\frac{nπR^2}{360°}$)