题目内容
9.一斜坡长为90m,它的高为15m,将重物从斜坡下起点推到斜坡上25m处停下,停下地点的高度为( )| A. | $\frac{25}{6}$m | B. | $\frac{23}{6}$m | C. | $\frac{6}{25}$m | D. | $\frac{5}{2}$m |
分析 根据题意画出图形,根据斜坡长90m,高为15m,求出sin∠A的值,然后根据AD=25m,求出DE的长度.
解答 解:如图所示,AD=25m,AB=90m,BC=15m,
过D作DE⊥AC于E,则DE∥BC,
则有sin∠A=$\frac{BC}{AB}$=$\frac{15}{90}$=$\frac{1}{6}$,
∵$\frac{DE}{AD}$=sin∠A=$\frac{1}{6}$,
∴DE=$\frac{1}{6}$×25=$\frac{25}{6}$(m).
故选A.
点评 本题考查了解直角三角形的应用,解答本题的关键是做出图形,根据已知求出sin∠A的值,然后利用三角函数求出DE的长度.

练习册系列答案
相关题目
4.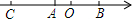 如图,数轴上A、B两点的数分别是-1和$\sqrt{3}$,点B、点C与点A的距离相等,则点C所表示的数为( )
如图,数轴上A、B两点的数分别是-1和$\sqrt{3}$,点B、点C与点A的距离相等,则点C所表示的数为( )
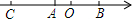 如图,数轴上A、B两点的数分别是-1和$\sqrt{3}$,点B、点C与点A的距离相等,则点C所表示的数为( )
如图,数轴上A、B两点的数分别是-1和$\sqrt{3}$,点B、点C与点A的距离相等,则点C所表示的数为( )| A. | -1-$\sqrt{3}$ | B. | -2+$\sqrt{3}$ | C. | -2-$\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
19.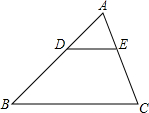 如图,在△ABC中,DE∥BC,S△ADE:S梯形DBCE=1:4,则AD:AB=( )
如图,在△ABC中,DE∥BC,S△ADE:S梯形DBCE=1:4,则AD:AB=( )
 如图,在△ABC中,DE∥BC,S△ADE:S梯形DBCE=1:4,则AD:AB=( )
如图,在△ABC中,DE∥BC,S△ADE:S梯形DBCE=1:4,则AD:AB=( )| A. | 1:2 | B. | 1:4 | C. | 1:25 | D. | $\sqrt{5}$:5 |
 请将下列证明过程中的理由或步骤补充完整:
请将下列证明过程中的理由或步骤补充完整: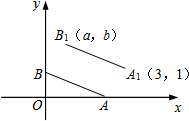 如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )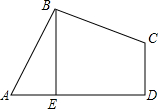 如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为4,则BE=( )
如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为4,则BE=( )