题目内容
2.已知抛物线y=x2-x-1与x轴的交点为(m,0),则代数式m2-m+2013的值为2014.分析 根据图象上点的坐标性质得出m2-m=1,进而代入求出即可.
解答 解:∵抛物线y=x2-x-1与x轴的一个交点为(m,0),
∴m2-m-1=0,
∴m2-m=1,
则代数式m2-m+2013=1+2013=2014.
故答案为:2014.
点评 此题主要考查了函数图象上点的坐标性质以及整体思想的应用,求出m2-m=1是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12. 如图,已知边长为2的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点,则是弦DE的长为( )
如图,已知边长为2的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点,则是弦DE的长为( )
 如图,已知边长为2的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点,则是弦DE的长为( )
如图,已知边长为2的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点,则是弦DE的长为( )| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{2\sqrt{10}}{5}$ | D. | $\frac{4\sqrt{5}}{5}$ |
10.($\sqrt{3}$-1)0+(-0.125)2014×82014的结果( )
| A. | $\sqrt{3}$ | B. | $\sqrt{3}$-2 | C. | 2 | D. | -2 |
14.在-34,0,28,-9这四个数中,绝对值最大的是( )
| A. | -34 | B. | -9 | C. | 0 | D. | 28 |
11.下列抛物线的顶点在第二象限的是( )
| A. | y=x2-x+2 | B. | y=x2+x+2 | C. | y=-x2-x+2 | D. | y=-x2+x+2 |
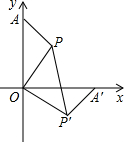 如图,在直角坐标系中,点A(0,5),点P(2,3),将△AOP绕点O顺时针方向旋转,使OA边落在x轴上,则点P'的坐标为(3,-2).
如图,在直角坐标系中,点A(0,5),点P(2,3),将△AOP绕点O顺时针方向旋转,使OA边落在x轴上,则点P'的坐标为(3,-2). 如图,直线y=-4x+4与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y=$\frac{k}{x}$(k≠0)上,则k=5.
如图,直线y=-4x+4与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y=$\frac{k}{x}$(k≠0)上,则k=5.