题目内容
17.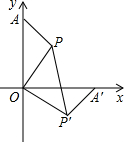 如图,在直角坐标系中,点A(0,5),点P(2,3),将△AOP绕点O顺时针方向旋转,使OA边落在x轴上,则点P'的坐标为(3,-2).
如图,在直角坐标系中,点A(0,5),点P(2,3),将△AOP绕点O顺时针方向旋转,使OA边落在x轴上,则点P'的坐标为(3,-2).
分析 如图,过点P作PE⊥x轴于点E,过点P′作P′F⊥y轴于点F,证△POE≌△P′OF可得P′F=PE=3,OF=OE=2,从而可得点P′的坐标.
解答 解:如图,过点P作PE⊥x轴于点E,过点P′作P′F⊥y轴于点F,
∴∠PEO=∠P′FO=90°,
由旋转可知∠POP′=90°,即∠POE+∠P′OA′=90°,OP=OP′,
又∵∠P′OA′+∠P′OF=90°,
∴∠POE=∠P′OF,
在△POE和△P′OF中,
∵$\left\{\begin{array}{l}{∠POE=∠P′OF}\\{∠PEO=∠P′FO}\\{PO=P′O}\end{array}\right.$,
∴△POE≌△P′OF(AAS),
∴P′F=PE=3,OF=OE=2,
∴点P′坐标为(3,-2),
故答案为:(3,-2).
点评 本题主要考查旋转的性质和全等三角形的判定与性质,熟练掌握旋转的性质以判定三角形全等是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
8. 某校对600名学生进行了一次“心理健康”知识测试,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本,绘制了如图尚未完成的表格和频数分布直方图(注:无50.5以下成绩)
某校对600名学生进行了一次“心理健康”知识测试,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本,绘制了如图尚未完成的表格和频数分布直方图(注:无50.5以下成绩)
(1)频数分布表中,A=80.5,B=16,C=0.2.
(2)补全频数分布直方图.
(3)若成绩在90分以上(不含90分)为优秀,试估计该校成绩优秀的有多少人?
 某校对600名学生进行了一次“心理健康”知识测试,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本,绘制了如图尚未完成的表格和频数分布直方图(注:无50.5以下成绩)
某校对600名学生进行了一次“心理健康”知识测试,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本,绘制了如图尚未完成的表格和频数分布直方图(注:无50.5以下成绩)| 分组 | 频数 | 频数 |
| 50.5~60.5 | 2 | 0.04 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 10 | C |
| A~90.5 | B | 0.32 |
| 90.5~100.5 | 14 | 0.28 |
| 合计 |
(2)补全频数分布直方图.
(3)若成绩在90分以上(不含90分)为优秀,试估计该校成绩优秀的有多少人?
5.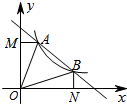 如图,已知直线y=-x+b(b>0)与双曲线y=$\frac{k}{x}$(x>0)交 于A、B两点,连接OA、OB,AM⊥y轴于点M,BN⊥x轴于点N,下列结论:①OA=OB;②△AOM≌△BON;③当AB=$\sqrt{2}$时,ON=BN=1.④若∠AOB=45°,则S△AOB=k;其中结论正确的是( )
如图,已知直线y=-x+b(b>0)与双曲线y=$\frac{k}{x}$(x>0)交 于A、B两点,连接OA、OB,AM⊥y轴于点M,BN⊥x轴于点N,下列结论:①OA=OB;②△AOM≌△BON;③当AB=$\sqrt{2}$时,ON=BN=1.④若∠AOB=45°,则S△AOB=k;其中结论正确的是( )
 如图,已知直线y=-x+b(b>0)与双曲线y=$\frac{k}{x}$(x>0)交 于A、B两点,连接OA、OB,AM⊥y轴于点M,BN⊥x轴于点N,下列结论:①OA=OB;②△AOM≌△BON;③当AB=$\sqrt{2}$时,ON=BN=1.④若∠AOB=45°,则S△AOB=k;其中结论正确的是( )
如图,已知直线y=-x+b(b>0)与双曲线y=$\frac{k}{x}$(x>0)交 于A、B两点,连接OA、OB,AM⊥y轴于点M,BN⊥x轴于点N,下列结论:①OA=OB;②△AOM≌△BON;③当AB=$\sqrt{2}$时,ON=BN=1.④若∠AOB=45°,则S△AOB=k;其中结论正确的是( )| A. | ②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
9.用科学记数法表示0.0000039,正确的是( )
| A. | 39×10-6 | B. | 3.9×10-6 | C. | 3.9×10-5 | D. | 39×10-5 |
