Question

15．如果一个等边三角形ABC的一边AB在y轴上，其顶点A在坐标原点．已知AB=1，求第三个顶点C的坐标．

Answer 1

分析 分四种情况，点C分别在四个象限内，画出图形，根据等边三角形的性质得出顶点C的坐标．

解答 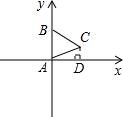解：当点C在第一象限时，过点C作CD⊥x轴，
∵△ABC是等边三角形，AB=1，
∴AB=AC=1，∠CAD=30°，
∴CD=，AD=$\frac{1}{2}$$\sqrt{3}$，
∴C（$\frac{1}{2}$$\sqrt{3}$，$\frac{1}{2}$）；
当点C在第二象限时，点C坐标与（$\frac{1}{2}$$\sqrt{3}$，$\frac{1}{2}$）关于y轴对称，从而得出第二个点C坐标（-$\frac{1}{2}$$\sqrt{3}$，$\frac{1}{2}$）；
从而得出另外两个点C坐标（-$\frac{1}{2}$$\sqrt{3}$，-$\frac{1}{2}$）；（$\frac{1}{2}$$\sqrt{3}$，-$\frac{1}{2}$），
所以第三个顶点C的坐标为（$\frac{1}{2}$$\sqrt{3}$，$\frac{1}{2}$）；（-$\frac{1}{2}$$\sqrt{3}$，-$\frac{1}{2}$）；（$\frac{1}{2}$$\sqrt{3}$，-$\frac{1}{2}$），（-$\frac{1}{2}$$\sqrt{3}$，$\frac{1}{2}$）．

点评 本题考查的是等边三角形的性质，根据题意画出图形，利用数形结合求解是解答此题的关键．