题目内容
 一直角三角形放置在如图的平面直角坐标系中,直角顶点C刚好落在双曲线y=
一直角三角形放置在如图的平面直角坐标系中,直角顶点C刚好落在双曲线y=| 8 |
| x |
考点:全等三角形的判定与性质,反比例函数系数k的几何意义
专题:
分析:作CE垂直x轴于点E,AF⊥CE于点F,CM垂直于y轴于点M,AC交x轴于点N,求出△AFC≌△CEB得到AF=CE=2
,再运用四边形CAOB的面积=正方形MOEC的面积.
| 2 |
解答: 解:作CE垂直x轴于点E,AF⊥CE于点F,CM垂直于y轴于点M,AC交x轴于点N,
解:作CE垂直x轴于点E,AF⊥CE于点F,CM垂直于y轴于点M,AC交x轴于点N,
∵∠NOA=∠NCB=90°,∠ANO=∠BNC,
∴△ANO∽△CNB,
∴∠NAO=∠NBC,
又∵AO∥CE,
∴∠NAO=∠ACF,
∴∠ACF=∠NBC也就是∠ACF=∠EBC
∵∠AFC=∠CEB=90°,AC=AB,
在△AFC和△CEB中,
,
∴△AFC≌△CEB(AAS),
∴AF=CE,
∴双曲线y=
在C点的横坐标等于纵坐标,
∴x=
,
解得x=2
,
∴AF=CE=OE=2
,
又∵△MAC的面积=△AFC的面积=△CEB的面积,
∴四边形CAOB的面积=正方形MOEC的面积=2
×2
=8,
故答案为:8.
 解:作CE垂直x轴于点E,AF⊥CE于点F,CM垂直于y轴于点M,AC交x轴于点N,
解:作CE垂直x轴于点E,AF⊥CE于点F,CM垂直于y轴于点M,AC交x轴于点N,∵∠NOA=∠NCB=90°,∠ANO=∠BNC,
∴△ANO∽△CNB,
∴∠NAO=∠NBC,
又∵AO∥CE,
∴∠NAO=∠ACF,
∴∠ACF=∠NBC也就是∠ACF=∠EBC
∵∠AFC=∠CEB=90°,AC=AB,
在△AFC和△CEB中,
|
∴△AFC≌△CEB(AAS),
∴AF=CE,
∴双曲线y=
| 8 |
| x |
∴x=
| 8 |
| x |
解得x=2
| 2 |
∴AF=CE=OE=2
| 2 |
又∵△MAC的面积=△AFC的面积=△CEB的面积,
∴四边形CAOB的面积=正方形MOEC的面积=2
| 2 |
| 2 |
故答案为:8.
点评:本题主要考查全等三角形的判定及性质与反比例函数的知识,解决本题的关键是把四边形CAOB的面积转化为正方形MOEC的面积.

练习册系列答案
相关题目
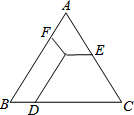 如图,△ABC是等边三角形,P是形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )
如图,△ABC是等边三角形,P是形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )| A、18 | ||
B、9
| ||
| C、6 | ||
| D、条件不够,不能确定 |
 如图,在△ABC中,∠ABC=60°,AB=3,BC=5,以AC为边在△ABC外作正△ACD,则BD的长为
如图,在△ABC中,∠ABC=60°,AB=3,BC=5,以AC为边在△ABC外作正△ACD,则BD的长为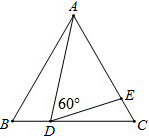 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且∠ADE=60°,若△ABC的边长为6,CD=2BD,则AD的长为
如图,△ABC是等边三角形,点D、E分别在BC、AC上,且∠ADE=60°,若△ABC的边长为6,CD=2BD,则AD的长为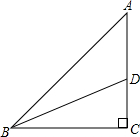 如图,在△ABC中,∠C=90°,点D在AC上,将△BCD沿BD翻折,点C落在斜边AB上,若AC=12cm,DC=5cm,则sinA=
如图,在△ABC中,∠C=90°,点D在AC上,将△BCD沿BD翻折,点C落在斜边AB上,若AC=12cm,DC=5cm,则sinA= 如图,△ABC中,AB=5,BC=11,tanB=
如图,△ABC中,AB=5,BC=11,tanB= 如图,在△ABC中,AB=AC,∠EDF=∠B,求证:△BDE∽△CFD.
如图,在△ABC中,AB=AC,∠EDF=∠B,求证:△BDE∽△CFD.