题目内容
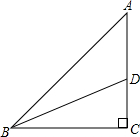如图，在△ABC中，∠C=90°，点D在AC上，将△BCD沿BD翻折，点C落在斜边AB上，若AC=12cm，DC=5cm，则sinA=考点：翻折变换（折叠问题）
专题：
分析：过D作DE⊥AB于点E，根据翻折可得∠ABD=∠CBD，再根据角平分线上的点到角的两边的距离相等可得DE=DC，从而得解．
解答：
解：如图，过D作DE⊥AB于点E，
∵△BCD沿BD翻折，点C落在斜边AB上，
∴∠ABD=∠CBD，
又∵∠C=90，
∴DE=DC，
∵DC=5cm，
∴DE=5cm，
∵AC=12cm，
∴AD=12-5=7cm，
∴在Rt△AED中，sinA=
=
．
故答案为：
．
解：如图，过D作DE⊥AB于点E，∵△BCD沿BD翻折，点C落在斜边AB上，
∴∠ABD=∠CBD，
又∵∠C=90，
∴DE=DC，
∵DC=5cm，
∴DE=5cm，
∵AC=12cm，
∴AD=12-5=7cm，
∴在Rt△AED中，sinA=
| DE |
| AD |
| 5 |
| 7 |
故答案为：
| 5 |
| 7 |
点评：本题考查了角平分线上的点到角的两边的距离相等的性质，翻折变换的性质，判断出∠ABD=∠CBD并熟记角平分线的性质是解题的关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
一直角三角形放置在如图的平面直角坐标系中，直角顶点C刚好落在双曲线y=
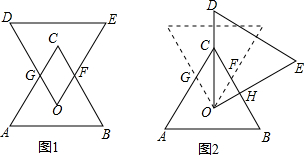如图（1），有两个全等的正三角形ABC和ODE，点O、C分别为△ABC、△DEO的重心；固定点O，将△ODE顺时针旋转，使得OD经过点C，如图（2），则图（2）中四边形OGCF与△OCH面积的比为下列条件中不能判定一定是平行四边形的有（ ）
| A、一组对角相等，一组邻角互补 |
| B、一组对边平行，另一组对边相等 |
| C、一组对边相等，一组对角相等 |
| D、一组对边平行，且一条对角线平分另一条对角 |