题目内容
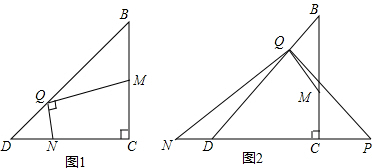
13.在一条公路旁有A、B两个工厂,要在公路旁修一个汽车站,请分别按如下要求确定汽车站M的位置:(1)在图①中,要求车站M到AB两厂的距离相等;
(2)在图②中,要求车站M到AB两厂的距离之和AM+BM最短;
(3)在图③中,要求车站M到AB两厂的距离之差AM-BM最大.
分析 (1)根据垂直平分线的性质即可解决问题.
(2)根据对称作图,利用两点之间线段最短解决问题.
(3)根据三角形两边之差小于第三边即可解决问题.
解答 解:(1)如图①中,作线段AB的垂直平分线交直线l于M,此时MA=MB.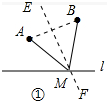
(2)如图②中,作点B关于直线l的对称点B′,连接AB′与直线l交于点M,此时MA+BM最小.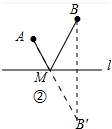
(3)如图③中,作点B关于直线l的对称点B′,连接AB′且延长AB′交直线l于点M,此时MA-BM最大.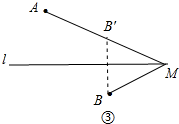
点评 本题考查作图与设计、垂线段最短、三角形两边之差小于第三边、两点之间线段最短等知识,解题的关键是灵活应用这些知识解决最值问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.多项式-π2x5-2x3y3+3x-5的次数是( )
| A. | 3 | B. | 5 | C. | 6 | D. | 7 |
2.解方程$\frac{2x-1}{3}$-1=$\frac{2-3x}{6}$时,去分母正确的是( )
| A. | 2(2x-1)-1=2-3x | B. | 6(2x+1)+6=3(2-3x) | C. | 6(2x+1)-1=3(2-3x) | D. | 2(2x-1)-6=2-3x |
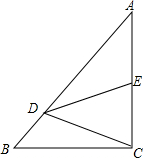 如图,在Rt△ABC中,∠ACB=90°,点D在边AB上,线段DC绕点D按逆时针旋转,端点C恰巧落在边AC上的点E处,已知$\frac{AD}{DB}$=4,求$\frac{AE}{EC}$的值.
如图,在Rt△ABC中,∠ACB=90°,点D在边AB上,线段DC绕点D按逆时针旋转,端点C恰巧落在边AC上的点E处,已知$\frac{AD}{DB}$=4,求$\frac{AE}{EC}$的值.