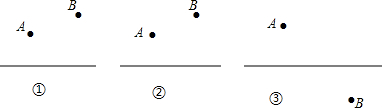题目内容
1.△BCD中,BC=CD,∠BCD=90°,点Q为BD上一点,M、N分别为直线BC、CD上一点,且∠MQN=90°.(1)如图1,若BQ=3DQ,求$\frac{QM}{QN}$的值;
(2)如图2,若DQ=3BQ,QP⊥BD交直线DC于点P,求$\frac{BM}{NP}$的值.
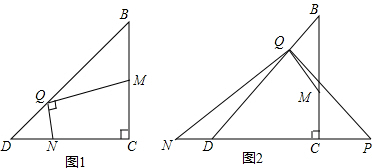
分析 (1)如图1,过Q点作QP⊥BD交DC于P,然后根据等腰直角三角形的性质的性质证明△QPN∽△QBM,就可以得出结论;
(2)根据余角的性质得到∠NQP=∠MQB,然后根据等腰直角三角形的性质的性质证明△QPN∽△QBM,就可以得出结论.
解答 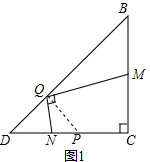 解:(1)如图1,过Q点作QP⊥BD交DC于P,
解:(1)如图1,过Q点作QP⊥BD交DC于P,
∴∠PQB=90°.
∵∠MQN=90°,
∴∠NQP=∠MQB,
∵CD=CB,∠BCD=90°,
∴∠DPQ=∠D=45°,DQ=PQ,
∴∠DPQ=∠DBC,
∴△QPN∽△QBM,
∴$\frac{QM}{QN}=\frac{BQ}{PQ}$,
∵BQ=3DQ,
∴BQ=3PQ,
∴$\frac{QM}{QN}$=$\frac{1}{3}$;
(2)∵QP⊥BD交DC于P,
∴∠PQD=90°.
∵∠MQN=90°,
∴∠NQP=∠MQB,
∵CD=CB,∠BCD=90°,
∴∠DPQ=∠D=45°,DQ=PQ,
∴∠DPQ=∠DBC,
∴△QPN∽△QBM,
∴$\frac{BM}{PN}$=$\frac{BQ}{PQ}$,
∵BQ=$\frac{1}{3}$DQ,
∴BQ=$\frac{1}{3}$PQ,
∴$\frac{BM}{PN}$=$\frac{1}{3}$.
点评 本题考查了相似三角形的判定与性质的运用,等腰直角三角形的性质,在解答时利用三角形相似的性质求出线段的比是解答本题的关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
10. 如图,在正方形ABCD内作等边△AED,连接AC,则∠EAC的度数为( )
如图,在正方形ABCD内作等边△AED,连接AC,则∠EAC的度数为( )
 如图,在正方形ABCD内作等边△AED,连接AC,则∠EAC的度数为( )
如图,在正方形ABCD内作等边△AED,连接AC,则∠EAC的度数为( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
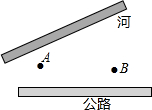 如图,公路与大河的中间地带有两个工厂A,B,现要在公路上建一仓库,在河边修一水泵站.
如图,公路与大河的中间地带有两个工厂A,B,现要在公路上建一仓库,在河边修一水泵站.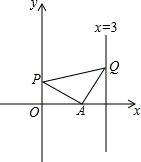 如图,在平面直角坐标系xOy中,点A的坐标为(2,0),Q是直线x=3上的一个动点,y轴正半轴上是否存在点P,使△APQ为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.
如图,在平面直角坐标系xOy中,点A的坐标为(2,0),Q是直线x=3上的一个动点,y轴正半轴上是否存在点P,使△APQ为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.