题目内容
5.学校有一块平行四边形的草地,现想把草地分成面积相等的两块,中间留一条小路,(1)想一想会有多少种分法,请你在图①②③中的平行四边形中画出满足条件的示意图.
(2)在上述问题中,明明看到草地中间的点P处有一块标志石,如图④,他建议经过标志石修小路,一样可以把草地分成面积相等的两部分.试一试,可以怎样分?并说明你的做法的正确性.

分析 (1)分别画对角线,过对边中点的直线即可.
(2)如图④中,连接AC、BD交于点O,作直线PO,直线PO即为所求,利用全等三角形的性质即可证明.
解答 (1)有无数种分法,图①、②画对角线,图③取对边中点.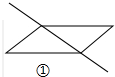
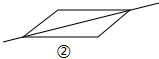
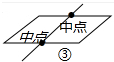
(2)如图④中,连接AC、BD交于点O,作直线PO,直线PO即为所求.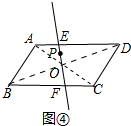
理由:设直线PO交AD于E,交BC于F,
∵四边形ABCD是平行四边形,
∴AD∥BC,AO=OC,
∴∠OAE=∠OCF,
在△AOE和△COF中,
$\left\{\begin{array}{l}{∠AOE=∠COF}\\{∠OAE=∠OCF}\\{AO=OC}\end{array}\right.$,
∴△AOE≌△COF,
∴S△AOE=S△COF,
∵S△ACB=S△ACD,
∴S四边形ABFE=S四边形CDEF.
∴直线OP把平行四边形ABCD的面积分成相等的两部分.
点评 本题考查平行四边形的性质、作图-应用与设计,解题的关键是灵活运用全等三角形的性质,记住过平行四边形的对角线的交点的直线把平行四边形分成面积相等的两部分,属于中考常考题型.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
10. 如图,在正方形ABCD内作等边△AED,连接AC,则∠EAC的度数为( )
如图,在正方形ABCD内作等边△AED,连接AC,则∠EAC的度数为( )
 如图,在正方形ABCD内作等边△AED,连接AC,则∠EAC的度数为( )
如图,在正方形ABCD内作等边△AED,连接AC,则∠EAC的度数为( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
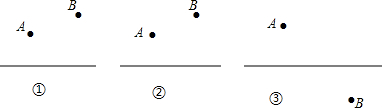
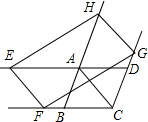 如图,直线EF与?ABCD的对角线AC平行,分别交DA,CB的延长线于点E,F,直线GH与AC平行,分别交CD,BA的延长线于点G,H,则EF与HG的关系是EF=HG,EF∥HG.
如图,直线EF与?ABCD的对角线AC平行,分别交DA,CB的延长线于点E,F,直线GH与AC平行,分别交CD,BA的延长线于点G,H,则EF与HG的关系是EF=HG,EF∥HG. 如图,点D、E分别在△ABC边BC、AC上,连接线段AD、BE交于点F,若AE:EC=1:3,BD:DC=2:3,则EF:FB=$\frac{3}{8}$.
如图,点D、E分别在△ABC边BC、AC上,连接线段AD、BE交于点F,若AE:EC=1:3,BD:DC=2:3,则EF:FB=$\frac{3}{8}$.