题目内容
14．若实数a，b，c满足等式2$\sqrt{a}$+3|b|=6，4$\sqrt{a}$-9|b|=6c，则c可能取的最大值为2．分析 将两等式组成关于$\sqrt{a}$和|b|方程组，求出其表达式（含c），再根据非负数的性质解答即可．
解答 解：由两个已知等式可得：$\sqrt{a}$=$\frac{3}{5}$（c+3），|b|=$\frac{2}{5}$（2-c），
而|b|≥0，所以c≤2．
当c=2时，可得a=9，b=0，满足已知等式．
所以c可能取的最大值为2．
故答案为：2．
点评 此题将非负数的性质与不等式组相结合，综合性较强．初中阶段的非负数的性质有三种：绝对值、偶次方、平方根，在解题时要注意加以灵活应用．
练习册系列答案
相关题目
小知识：古希腊的毕达哥拉斯，在2500年前曾经大胆断言，一条线段（AB）的某一部分（AC）与另一部分（BC）之比，如果正好等于另一部分（BC）同整个线段（AB）的比（即BC2=AC．AB），那么这样的比例会给人一种美感，后来我们将分割这条线段（AB）的点C称为线段AB的“黄金分割点”，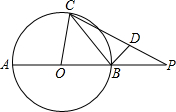
如图，AB是⊙O的直径，延长AB至P，使BP=OB，BD垂直于弦BC，垂足为点B，点D在PC上．设∠PCB=α，∠POC=2β．求证：tanα•tanβ=$\frac{1}{3}$．