Question

8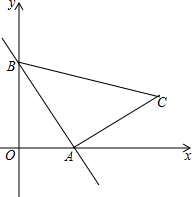．如图，在平面直角坐标系中，点C的坐标为（3，1），动点A以每秒1个单位的速度从点O出发沿x轴正半轴运动，同时动点B以每秒2个单位的速度从点O出发沿y轴正半轴运动，作直线AB．设运动的时间为t秒，是否存在t，使△ABC是等腰三角形？若存在，求t的值；若不存在，请说明理由．

Answer 1

分析 运动的时间是t，则OA=t，OB=2t，利用勾股定理把AB²，BC²和AC²用t表示出来，然后利用勾股定理列方程求得t的值，然后判断t是否满足条件，以及是否是等腰三角形即可．

解答 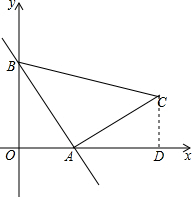解：运动的时间是t，则OA=t，OB=2t．
在直角△OAB中，AB²=OA²+OB²=t²+（2t）²=5t²，
过C作CD⊥x轴于点D，则D的坐标是（3，0）．
在直角△ACD中，AC²=CD²+AD²=1+（3-t）²=t²-6t+10，
BC²=3²+（2t-1）²=4t²-4t+10，
当AB是斜边时，AB²=AC²+BC²，则5t²=t²-6t+10+4t²-4t+10，
解得：t=2．
此时AB²=20，AC²=2，BC²=18，此时不是等腰三角形，故不符合条件；
当AC是斜边时，AC²=AB²+BC²，则t²-6t+10=5t2+（4t²-4t+10），
解得：t=0或-4（不符合题意，舍去）；
当BC是斜边时，AB²+AC²=BC²，则5t²+（t²-6t+10）=4t²-4t+10，
解得：t=0（舍去），或1．
当t=1时，AB²=5，AC²=1-6+10=5，此时AB=AC．
总之，当t=1时，△ABC是等腰直角三角形．

点评 本题考查了一次函数与勾股定理的综合应用，正确进行讨论，利用m表示出AB²，BC²和AC²是关键．