题目内容
16. 如图,点A(m,m+1),B(m+3,m-1)是反比例函数y=$\frac{k}{x}$(x>0)与一次函数y=ax+b的交点,求:
如图,点A(m,m+1),B(m+3,m-1)是反比例函数y=$\frac{k}{x}$(x>0)与一次函数y=ax+b的交点,求:(1)一次函数的解析式;
(2)根据图象直接写出不等式$\frac{k}{x}>ax+b$的解集.
分析 (1)根据反比例函数的特点k=xy为定值,列出方程,求出m的值,便可求出反比例函数的解析式;根据m的值求出A、B两点的坐标,用待定实数法便可求出一次函数的解析式.
(2)根据函数图象可直接解答.
解答 解:(1)由题意可知,m(m+1)=(m+3)(m-1).
解,得m=3.(2分)
∴A(3,4),B(6,2);
∴k=4×3=12,
∴y=$\frac{12}{x}$.
∵A点坐标为(3,4),B点坐标为(6,2),
∴$\left\{\begin{array}{l}{3a+b=4}\\{6a+b=2}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=6}\end{array}\right.$,
∴y=-$\frac{2}{3}$x+6.
(2)根据图象得x的取值范围:0<x<3或x>6.
点评 此题考查的是反比例函数与一次函数的交点问题,掌握反比例函数图象上点的坐标特点及用待定系数法求一次函数及反比例函数的解析式是解题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
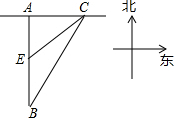 阅读材料,回答问题
阅读材料,回答问题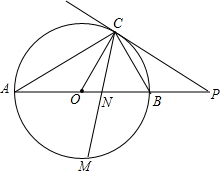 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
 现有长方形纸片一张,长19cm,宽15cm,需要剪去边长是多少的小正方形才能做成底面积为77cm2的无盖长方体型的纸盒?
现有长方形纸片一张,长19cm,宽15cm,需要剪去边长是多少的小正方形才能做成底面积为77cm2的无盖长方体型的纸盒?