题目内容
 如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.(1)图中是否存在与△ODM相似的三角形?若存在,请找出并给于证明.
(2)设DM=x,OA=R,求R关于x 的函数关系式;是否存在整数R,使得利用正方形ABCD内部的扇形OAM围成的圆锥地面周长可以为4π?若存在请求出此时DM的长;不存在,请说明理由.
(3)在动点O逐渐向点D运动(OA逐渐增大)的过程中,△CMN的周长如何变化?说明理由.
考点:圆的综合题
专题:
分析:(1)可以选择证明△ODM∽△MCN;
(2)先利用勾股定理求出R关于x的表达式,再由R的取值范围,分别讨论求解;
(3)根据△ODM∽△MCN,利用对应边成比例得出CN,同理得出MN,表示出△CMN的周长,即可作出判断.
(2)先利用勾股定理求出R关于x的表达式,再由R的取值范围,分别讨论求解;
(3)根据△ODM∽△MCN,利用对应边成比例得出CN,同理得出MN,表示出△CMN的周长,即可作出判断.
解答:解:(1)∵MN切⊙O于点M,
∴∠OMN=90°,
∵∠OMD+∠CMN=90°,∠CMN+∠CNM=90°,
∴∠OMD=∠MNC,
又∵∠D=∠C=90°,
∴△ODM∽△MCN.

(2)在Rt△ODM中,DM=x,设OA=OM=R,
∴OD=AD-OA=8-R,
由勾股定理得:(8-R)2+x2=R2,
∴64-16R+R2+x2=R2,
∴OA=R=
,
∵4<OA<8,即4<R<8,
∴当R=5时,∠MOA超过1800,不符合,舍去,
当R=6时,∠MOA=120°,
∴x=±4
,
∵x>0,
∴x=4
,
同理当R=7时,x=
.
(3)∵CM=CD-DM=8-x,OD=8-R=8-
,
且有△ODM∽△MCN,
∴
=
,
∴代入得到:CN=
,
同理
=
,
∴代入得到:MN=
,
∴△CMN的周长为P=CM+CN+MN=(8-x)+
+
=(8-x)+(x+8)=16,
在点O的运动过程中,△CMN的周长始终为16,是一个定值.
∴∠OMN=90°,
∵∠OMD+∠CMN=90°,∠CMN+∠CNM=90°,
∴∠OMD=∠MNC,
又∵∠D=∠C=90°,
∴△ODM∽△MCN.

(2)在Rt△ODM中,DM=x,设OA=OM=R,
∴OD=AD-OA=8-R,
由勾股定理得:(8-R)2+x2=R2,
∴64-16R+R2+x2=R2,
∴OA=R=
| x2+64 |
| 16 |
∵4<OA<8,即4<R<8,
∴当R=5时,∠MOA超过1800,不符合,舍去,
当R=6时,∠MOA=120°,
∴x=±4
| 2 |
∵x>0,
∴x=4
| 2 |
同理当R=7时,x=
| 38 |
(3)∵CM=CD-DM=8-x,OD=8-R=8-
| x2+64 |
| 16 |
且有△ODM∽△MCN,
∴
| MC |
| OD |
| CN |
| DM |
∴代入得到:CN=
| 16x |
| x+8 |
同理
| MC |
| OD |
| MN |
| OM |
∴代入得到:MN=
| x2+64 |
| x+8 |
∴△CMN的周长为P=CM+CN+MN=(8-x)+
| 16x |
| x+8 |
| x2+64 |
| x+8 |
在点O的运动过程中,△CMN的周长始终为16,是一个定值.
点评:本题考查了圆的综合,涉及了勾股定理、切线的性质、相似三角形的判定与性质,综合的知识点较多,此类题目对学生的综合能力要求较高,注意掌握数形结合思想、分类讨论思想的运用.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目

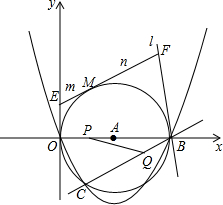 如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2+bx+c(a≠0)过O、B、C三点,B、C坐标分别为(10,0)和(
如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2+bx+c(a≠0)过O、B、C三点,B、C坐标分别为(10,0)和( 在梯形ABCD中,AD∥BC,AB=DC=3cm,BC=4cm,∠B=∠C=60°,点P从点A开始沿AB边向点B运动,Q从C沿CD向D运动,过点Q作QE∥AB交BC于点E,连接AQ,PE,若点P,Q同时出发且均以1cm/s的速度运动.
在梯形ABCD中,AD∥BC,AB=DC=3cm,BC=4cm,∠B=∠C=60°,点P从点A开始沿AB边向点B运动,Q从C沿CD向D运动,过点Q作QE∥AB交BC于点E,连接AQ,PE,若点P,Q同时出发且均以1cm/s的速度运动.
 如图,点D是△ABC的边AB上的一点,CN∥AB,DN交AC于点P,若PA=PC.求证:CD=AN.
如图,点D是△ABC的边AB上的一点,CN∥AB,DN交AC于点P,若PA=PC.求证:CD=AN.