题目内容
11.关于x的一元二次方程x2+bx+2=0有两个不相等的实数根,写出一个满足条件的实数b的值:b=3.分析 根据题意可知判别式△=b2-8>0,从而求得b的取值范围,然后即可得出答案.
解答 解:∵关于x的一元二次方程x2+bx+2=0有两个不相等的实数根,
∴△=b2-8>0,
∴b>2$\sqrt{2}$或b<-2$\sqrt{2}$,
∴b为3,4,5等等,
∴b为3(答案不唯一).
故答案为3.
点评 此题主要考查了一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.一次数学测验中,某小组五位同学的成绩分别是:110,105,90,95,90,则这五个数据的中位数是( )
| A. | 90 | B. | 95 | C. | 100 | D. | 105 |
19.互为相反数的两个数的和为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
4.分式$\frac{1}{x-2}$有意义,则x的取值范围是( )
| A. | x>2 | B. | x=2 | C. | x≠2 | D. | x<2 |
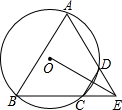 如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE.
如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE.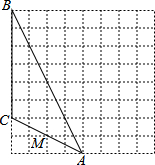 如图是一个由8×8个小正方形组成的方格纸,我们把顶点在正方形顶点的三角形称为格点三角形,图中的△ABC就是一个格点三角形,点M是AC的中点.
如图是一个由8×8个小正方形组成的方格纸,我们把顶点在正方形顶点的三角形称为格点三角形,图中的△ABC就是一个格点三角形,点M是AC的中点.