题目内容
17.如果$\frac{b}{a-b}$=$\frac{8}{3}$,则$\frac{a+b}{b}$=$\frac{19}{8}$.分析 根据已知条件设b=8k.a-b=3k,代入代数式即可结论.
解答 解:∵$\frac{b}{a-b}$=$\frac{8}{3}$,
设b=8k.a-b=3k,
∴a=11k,
∴$\frac{a+b}{b}$=$\frac{19}{8}$,
故答案为:$\frac{19}{8}$.
点评 此题主要考查了比例的性质,关键是掌比例的性质.

练习册系列答案
相关题目
7.图中的各曲线中,不表示y是x的函数是( )
| A. |  | B. |  | C. |  | D. |  |
5.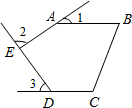 如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3=( )
如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3=( )
 如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3=( )
如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3=( )| A. | 90° | B. | 180° | C. | 120° | D. | 270° |
12.计算题.
| (1)(-2)+(-7); | (2)-32-5; | (3)(-30.5)×0.2; |
| (4)12-(-18)+(-7)-15; | (5)(-$\frac{3}{4}$)×(-1$\frac{1}{2}$)×0÷(-2$\frac{1}{4}$); | (6)-9×(-11)÷3÷(-3); |
| (7)-18÷2$\frac{1}{4}$-$\frac{4}{9}$÷(-$\frac{2}{3}$); | (8)($\frac{9}{10}$-$\frac{2}{15}$+$\frac{1}{6}$)×30; | (9)1-3.9÷[1-$\frac{3}{4}$-(-0.5)]. |
8.$\sqrt{7}$的范围是( )
| A. | 1<$\sqrt{7}$<2 | B. | 2<$\sqrt{7}$<3 | C. | 3<$\sqrt{7}$<4 | D. | 3<$\sqrt{7}$<5 |
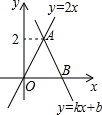 如图,函数y=kx+b(k≠0)的图象经过点B,与函数y=2x的图象交于点A,若△AOB的面积为2,则b等于( )
如图,函数y=kx+b(k≠0)的图象经过点B,与函数y=2x的图象交于点A,若△AOB的面积为2,则b等于( )