题目内容
17.已知关于x的方程$\frac{x}{x-2}-\frac{m}{2-x}=-1$的解大于1,则实数m的取值范围是m<0,且m≠-2.分析 先解方程$\frac{x}{x-2}-\frac{m}{2-x}=-1$,再利用方程的解大于1,且x≠2求解即可.
解答 解:方程两边乘x-2得:x+m=2-x,
移项得:2x=2-m,
系数化为1得:x=$\frac{2-m}{2}$,
∵方程的解大于1,
∴$\frac{2-m}{2}$>1,且$\frac{2-m}{2}$≠2,解得m<0,且m≠-2.
故答案为:m<0,且m≠-2.
点评 本题主要考查了分式方程的解,解题的关键是不要漏掉分式方程有意义的条件.

练习册系列答案
相关题目
8.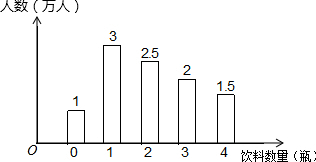 某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成图
某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成图
(1)在A出口的被调查游客中,购买2瓶及2瓶以上饮料的游客人数占A出口的被调查游客人数的60%.
表一
(2)试问A出口的被调查游客在园区内人均购买了多少瓶饮料?
(3)已知B、C两个出口的被调查游客在园区内人均购买饮料的数量如表一所示 若C出口的被调查人数比B出口的被调查人数多2万,且B、C两个出口的被调查游客在园区内共购买了49万瓶饮料,试问B出口的被调查游客人数为多少万?
 某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成图
某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成图(1)在A出口的被调查游客中,购买2瓶及2瓶以上饮料的游客人数占A出口的被调查游客人数的60%.
表一
| 出 口 | B | C |
| 人均购买饮料数量(瓶) | 3 | 2 |
(3)已知B、C两个出口的被调查游客在园区内人均购买饮料的数量如表一所示 若C出口的被调查人数比B出口的被调查人数多2万,且B、C两个出口的被调查游客在园区内共购买了49万瓶饮料,试问B出口的被调查游客人数为多少万?
12.下列性质中,正方形具有而菱形不一定具有的性质是( )
| A. | 四条边相等 | B. | 对角线互相平分 | C. | 对角线相等 | D. | 对角线互相垂直 |
9.“龟鹤同池,龟鹤共100只,共有脚350只,问龟鹤各多少只?”设龟有x只,鹤有y只,则下列方程组中正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=100}\\{2x+4y=350}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=100}\\{4x+2y=350}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-y=100}\\{4x+2y=350}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y=100}\\{2x+4y=350}\end{array}\right.$ |
7. 如图中,利用面积的等量关系验证的公式是( )
如图中,利用面积的等量关系验证的公式是( )
 如图中,利用面积的等量关系验证的公式是( )
如图中,利用面积的等量关系验证的公式是( )| A. | a2-b2=(a+b)(a-b) | B. | (a-b)2=a2-2ab+b2 | ||
| C. | (a+2b)(a-b)=a2+ab-2b2 | D. | (a+b)2=a2+2ab+b2 |
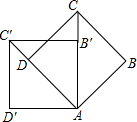 如图,正方形ABCD旋转后得到正方形AB′C′D′,①旋转角是45度;②若AB=1,则C′D=$\sqrt{2}$-1.
如图,正方形ABCD旋转后得到正方形AB′C′D′,①旋转角是45度;②若AB=1,则C′D=$\sqrt{2}$-1.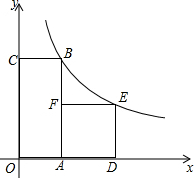 如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半釉上,点F在AB上,点B、E在反比例函数$y=\frac{k}{x}$的图象上OA=1,OC=4.
如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半釉上,点F在AB上,点B、E在反比例函数$y=\frac{k}{x}$的图象上OA=1,OC=4.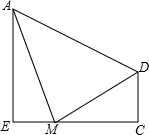 如图,直角梯形ABCD中,AE∥CD,∠E=90°,AE=CE=12,M为EC上一点,若∠MAD=45°,DM=10,求EM的长.
如图,直角梯形ABCD中,AE∥CD,∠E=90°,AE=CE=12,M为EC上一点,若∠MAD=45°,DM=10,求EM的长.