题目内容
17.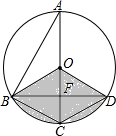 如图,已知在⊙O中,AB=2$\sqrt{3}$,AC是⊙O的直径,AC⊥BD于F,∠ABD=60°.
如图,已知在⊙O中,AB=2$\sqrt{3}$,AC是⊙O的直径,AC⊥BD于F,∠ABD=60°.(1)求图中阴影部分的面积;
(2)若用阴影部分围成一个圆锥侧面,请求出这个圆锥的底面圆的半径.
分析 (1)根据垂径定理,由AC⊥BD得弧BC=弧CD,且∠AFB=90°,则∠BAF=30°,利用圆周角定理得∠BOC=∠COD=60°,再由AC为直径得到∠ABC=90°,于是根据含30度的直角三角形三边的关系得到BC=$\frac{\sqrt{3}}{3}$AB=2,则OB=BC=2,然后根据扇形面积公式求解;
(2)设这个圆锥的底面圆的半径为r,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长和扇形面积公式得到$\frac{1}{2}$•2πr•2=$\frac{4}{3}$π,然后解关于r的方程即可.
解答 解:(1)∵AC⊥BD,
∴∠AFB=90°,弧BC=弧CD,
在Rt△ABF中,∵∠ABD=60°,
∴∠BAF=30°,
∴∠BOC=∠COD=2∠A=60°,
∵AC为直径,
∴∠ABC=90°,
∴BC=$\frac{\sqrt{3}}{3}$AB=$\frac{\sqrt{3}}{3}$×2$\sqrt{3}$=2,
∴OB=BC=2,
∴图中阴影部分的面积=$\frac{120•π•{2}^{2}}{360}$=$\frac{4}{3}$π;
(2)设这个圆锥的底面圆的半径为r,
∴$\frac{1}{2}$•2πr•2=$\frac{4}{3}$π,
∴r=$\frac{2}{3}$,
即这个圆锥的底面圆的半径为$\frac{2}{3}$.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了扇形面积的计算.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
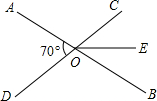 如图,直线AB、CD相交于点O,∠AOD=70°,OE平分∠BOC,求∠DOE的度数.
如图,直线AB、CD相交于点O,∠AOD=70°,OE平分∠BOC,求∠DOE的度数.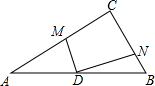 在△ABC中,∠C=90°,D为AB的中点,过点D作DM⊥DN,使DM交AC于M,DN交BC于N,求证:MN2=BN2+AM2.
在△ABC中,∠C=90°,D为AB的中点,过点D作DM⊥DN,使DM交AC于M,DN交BC于N,求证:MN2=BN2+AM2.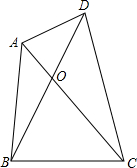 如图,S△AOD=3,S△AOB=4,S△COD=6,求S△BOC.
如图,S△AOD=3,S△AOB=4,S△COD=6,求S△BOC.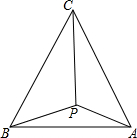 如图所示,P是正三角形ABC内一点,PA=2,PB=2$\sqrt{3}$,PC=4,求BC的长.
如图所示,P是正三角形ABC内一点,PA=2,PB=2$\sqrt{3}$,PC=4,求BC的长.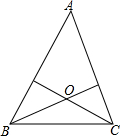 已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC,如图,若点O在△ABC的内部,求证:∠ABO=∠ACO.
已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC,如图,若点O在△ABC的内部,求证:∠ABO=∠ACO.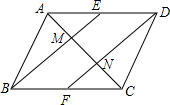 如图,在平行四边形ABCD中E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N.请你结合上述条件,写出两个你认为正确且与M、N有关的结论:
如图,在平行四边形ABCD中E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N.请你结合上述条件,写出两个你认为正确且与M、N有关的结论: