题目内容
5.已知函数y=2x+1和y=-x-2的图象交于点P,点P的坐标为(-1,-1),则方程组$\left\{\begin{array}{l}2x-y+1=0\\ x+y+2=0\end{array}\right.$的解为$\left\{\begin{array}{l}x=-1\\ y=-1\end{array}\right.$.分析 根据一次函数与二元一次方程组的关系求解.
解答 解:因为函数y=2x+1和y=-x-2的图象交于点P,点P的坐标为(-1,-1),
则方程组$\left\{\begin{array}{l}2x-y+1=0\\ x+y+2=0\end{array}\right.$的解$\left\{\begin{array}{l}x=-1\\ y=-1\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}x=-1\\ y=-1\end{array}\right.$
点评 本题考查了一次函数与二元一次方程(组),关键是根据两一次函数的交点坐标是两函数解析式所组成的方程组的解.

练习册系列答案
相关题目
15.圆的面积公式S=πR2中,S与R之间的关系是( )
| A. | S是R的正比例函数 | B. | S是R的一次函数 | ||
| C. | S是R的二次函数 | D. | 以上答案都不对 |
10.一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如表:
(1)求这个二次函数的表达式;
(2)求m的值.
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -$\frac{7}{2}$ | 0 | $\frac{5}{2}$ | 4 | $\frac{9}{2}$ | 4 | m | 0 | … |
(2)求m的值.
17.下列命题是假命题的是( )
| A. | 实数与数轴上的点一一对应 | |
| B. | 如果两个数的绝对值相等,那么这两个数必定也相等 | |
| C. | 对顶角相等 | |
| D. | 三角形的重心是三角形三条中线的交点 |
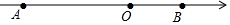 如图,点O为原点,A、B为数轴上两点,AB=15,且OA:OB=2.
如图,点O为原点,A、B为数轴上两点,AB=15,且OA:OB=2.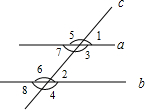 如图,直线a、b与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°,其中能判断a∥b的条件有( )
如图,直线a、b与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°,其中能判断a∥b的条件有( )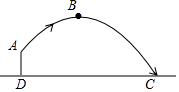 体育测试时,九年级一名学生,双手扔实心球.已知实心球所经过的路线是某个二次函数图象的一部分,如果球出手处A点距离地面的高度为2m,当球运行的水平距离为4m时,达到最大高度4m的B处(如图),问该学生把实心球扔出多远?(结果保留根号)
体育测试时,九年级一名学生,双手扔实心球.已知实心球所经过的路线是某个二次函数图象的一部分,如果球出手处A点距离地面的高度为2m,当球运行的水平距离为4m时,达到最大高度4m的B处(如图),问该学生把实心球扔出多远?(结果保留根号)