题目内容
1.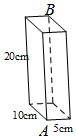 如图,长方体的长为10cm,宽为5cm,高为20cm.若一只蚂蚁沿着长方体的表面从点A爬到点B,需要爬行的最短路径是( )
如图,长方体的长为10cm,宽为5cm,高为20cm.若一只蚂蚁沿着长方体的表面从点A爬到点B,需要爬行的最短路径是( )| A. | 20+5$\sqrt{5}$ | B. | 25 | C. | 10$\sqrt{5}$+5 | D. | $5\sqrt{21}$ |
分析 作此题要把这个长方体中,蚂蚁所走的路线放到一个平面内,在平面内线段最短,根据勾股定理即可计算.
解答 解:第一种情况:把我们所看到的左面和上面组成一个平面,
则这个长方形的长和宽分别是10cm和15cm,
则所走的最短线段是$\sqrt{1{0}^{2}+1{5}^{2}}=5\sqrt{13}$cm;
第二种情况:把我们看到的前面与上面组成一个长方形,
则这个长方形的长和宽分别是30cm和5cm,
所以走的最短线段是$\sqrt{3{0}^{2}+{5}^{2}}=5\sqrt{37}$cm;
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是15cm和20cm,
所以走的最短线段是$\sqrt{1{5}^{2}+2{0}^{2}}=25$cm;
三种情况比较而言,第三种情况最短.
故选B
点评 本题考查了勾股定理的拓展应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.

练习册系列答案
相关题目
9.某中学七年级共400人,在期末统考后对本次考试中数学测验情况进行抽样了解,下列抽取的样本最合理的是( )
| A. | 抽取前50名同学的数学成绩 | |
| B. | 抽取后50名同学的数学成绩 | |
| C. | 抽取5班同学的数学成绩 | |
| D. | 抽取各班学好为5的倍数的同学的数学成绩 |
6. 如图,在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则BC的长度为( )
如图,在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则BC的长度为( )
 如图,在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则BC的长度为( )
如图,在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则BC的长度为( )| A. | 2 | B. | 8 | C. | $4\sqrt{3}$ | D. | $4\sqrt{5}$ |
10.一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如表:
(1)求这个二次函数的表达式;
(2)求m的值.
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -$\frac{7}{2}$ | 0 | $\frac{5}{2}$ | 4 | $\frac{9}{2}$ | 4 | m | 0 | … |
(2)求m的值.
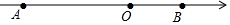 如图,点O为原点,A、B为数轴上两点,AB=15,且OA:OB=2.
如图,点O为原点,A、B为数轴上两点,AB=15,且OA:OB=2.