题目内容
1．
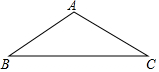如图，某厂房人字架屋顶的上弦AB=AC=10米，∠β=α，则该屋顶的跨度BC为（ ）| A． | 10sinα米 | B． | 10cosα米 | C． | 20sinα米 | D． | 20cosα米 |
分析 作AD⊥BC于点D，由等腰三角形的性质可得BC=2BD=2CD，在Rt△ABD中BD=ABcosB=10cosα，继而可得答案．
解答 解：如图，作AD⊥BC于点D，
∵AB=AC=10米，
∴BC=2BD=2CD，
∵在Rt△ABD中，∠B=α，
∴BD=ABcosB=10cosα，
则BC=2BD=20cosα，
故选：D．
点评 本题主要考查解直角三角形的应用和等腰三角形的性质，解答本题的关键是利用余弦函数的知识求出BD的长度．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在平面直角坐标系中，⊙P的圆心P的坐标为（a，4），半径为2，函数y=x的图象被⊙P截得的弦AB的长为$2\sqrt{3}$，则a的值为4-$\sqrt{2}$或4+$\sqrt{2}$．
9．我校为了纪念“一二•九”举办了八年级红歌合唱比赛，为了保证这次比赛的公正性，规定：参赛班级的基本素养、精神面貌、服装三项打分分别按5：3：2的比例计入总评成绩．二班、三班、五班的基本素养、精神面貌、服装的打分如下表，计算哪个班是第一名？
| 基本素养 | 精神面貌 | 服装 | |
| 二班 | 90 | 96 | 93 |
| 三班 | 90 | 90 | 96 |
| 五班 | 96 | 94 | 90 |
如图，A、B两城市相距80km，现计划在这两座城市间修建一条高速公路（即线段AB），经测量，森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上，已知森林保护区的范围在以P点为圆心，50km为半径的圆形区域内，请问计划修建的这条高速公路会不会穿越保护区，为什么？（参考数据：$\sqrt{3}$≈1.732，$\sqrt{2}$≈1.414）
6．
如图，若∠A=27°，∠B=45°，∠C=38°，则∠DFE等于（ ）
如图，若∠A=27°，∠B=45°，∠C=38°，则∠DFE等于（ ）| A． | 110° | B． | 115° | C． | 120° | D． | 125° |
