题目内容
11. 在平面直角坐标系中,⊙P的圆心P的坐标为(a,4),半径为2,函数y=x的图象被⊙P截得的弦AB的长为$2\sqrt{3}$,则a的值为4-$\sqrt{2}$或4+$\sqrt{2}$.
在平面直角坐标系中,⊙P的圆心P的坐标为(a,4),半径为2,函数y=x的图象被⊙P截得的弦AB的长为$2\sqrt{3}$,则a的值为4-$\sqrt{2}$或4+$\sqrt{2}$.
分析 分为两种情况:①当P在直线y=x的左边时,过P1D⊥AB于D,由垂径定理求出AD、由勾股定理求出P1D,过P1作P1D∥直线y=x,交y轴于D,过D作DB⊥直线y=x于B,得出DB=P1D=1,OB=DB=1,由勾股定理求出DO,得出直线P1D的解析式是y=x+$\sqrt{2}$,把P(a,4)代入求出a即可;②与①解法类似,当P在直线y=x的右边时,同法得出直线的解析式y=x-$\sqrt{2}$,把p(a,4)代入求出a的另一个值.
解答 解:分为两种情况: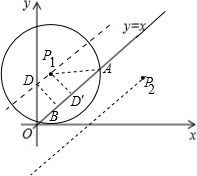
①当P在直线y=x的左边时,过P1D′⊥AB于D′,
由垂径定理得:AD′=$\frac{1}{2}$×2$\sqrt{3}$=$\sqrt{3}$,
∵P1A=2,由勾股定理得:P1D′=1,
过P1作P1D∥直线y=x,交y轴于D,过D作DB⊥直线y=x于B,则DB=P1D=1,
∵直线y=x,
∴∠DOB=45°,
∴OB=DB=1,由勾股定理得:DO=$\sqrt{2}$,
∵直线P1D∥直线y=x,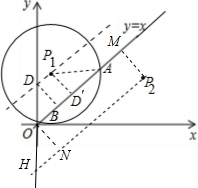 ∴直线P1D的解析式是y=x+$\sqrt{2}$(即把直线y=x相上平移$\sqrt{2}$个单位),
∴直线P1D的解析式是y=x+$\sqrt{2}$(即把直线y=x相上平移$\sqrt{2}$个单位),
∴把P(a,4)代入得:4=a+$\sqrt{2}$,
∴a=4-$\sqrt{2}$,
②当P在直线y=x的右边时,与①解法类似,P2M=ON=1,
由勾股定理得OH=$\sqrt{2}$,
把直线y=x向下平移$\sqrt{2}$个单位得出直线y=x-$\sqrt{2}$,
把p(a,4)代入求出a的另一个值是4+$\sqrt{2}$.
故答案为:4-$\sqrt{2}$或4+$\sqrt{2}$.
点评 本题考查了等腰三角形性质和判定,勾股定理,坐标与图形性质,垂径定理等知识点,主要考查学生的分析问题和解决问题的能力,注意:此题要进行分类讨论.

 阅读快车系列答案
阅读快车系列答案| A. | 无解 | B. | 有一组解 | C. | 有无穷多解 | D. | 不确定 |
(1)$\frac{1}{{a}^{2}b}$,$\frac{1}{a{b}^{2}}$;
(2)$\frac{2}{{x}^{2}+x}$,$\frac{4}{3{x}^{2}-6x}$.
| A. | 0 | B. | 1 | C. | 1-$\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$-1 |
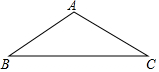 如图,某厂房人字架屋顶的上弦AB=AC=10米,∠β=α,则该屋顶的跨度BC为( )
如图,某厂房人字架屋顶的上弦AB=AC=10米,∠β=α,则该屋顶的跨度BC为( )| A. | 10sinα米 | B. | 10cosα米 | C. | 20sinα米 | D. | 20cosα米 |
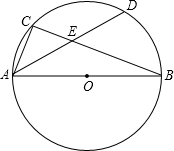 如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=10,AD=8,则AE的长为$\frac{7}{2}$.
如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=10,AD=8,则AE的长为$\frac{7}{2}$. 如图所示,点A在直线a外,点B在直线a上,在直线a上找一点P,使AP+BP最小的点P有1个,其位置是B点.
如图所示,点A在直线a外,点B在直线a上,在直线a上找一点P,使AP+BP最小的点P有1个,其位置是B点.