题目内容
11．求函数y=$\frac{3{x}^{2}+x+2}{{x}^{2}+2x+1}$的最小值．分析 将函数整理成关于x的一元二次方程，然后利用根的判别式列出不等式求解即可．
解答 解：∵y=$\frac{3{x}^{2}+x+2}{{x}^{2}+2x+1}$，
∴y（x2+2x+1）=3x2+x+2，
整理得，（y-3）x2+（2y-1）x+（y-2）=0，
∵关于x的一元二次方程有解，
∴△=b2-4ac=（2y-1）2-4（y-3）（y-2）≥0，
整理得，16y-24≥0，
解得y≤$\frac{3}{2}$，
所以，函数的最小值为$\frac{3}{2}$．
点评 本题考查了二次函数的最值，题目难度较大，将函数整理成关于x的一元二次方程并考虑利用根的判别式求解是解题的关键．
练习册系列答案
相关题目
1．
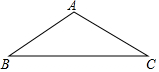如图，某厂房人字架屋顶的上弦AB=AC=10米，∠β=α，则该屋顶的跨度BC为（ ）
如图，某厂房人字架屋顶的上弦AB=AC=10米，∠β=α，则该屋顶的跨度BC为（ ）| A． | 10sinα米 | B． | 10cosα米 | C． | 20sinα米 | D． | 20cosα米 |
2．某商店一周内甲、乙两种计算器每天的销售量如下（单位：个）：
（1）将表格填写完整．
（2）求甲种计算器本周销售量的方差．
（3）已知乙种计算器本周销售量的方差为$\frac{8}{7}$，本周哪种计算器的销售量比较稳定？说明理由．
| 类别/星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 平均数 |
| 甲 | 3 | 4 | 4 | 3 | 4 | 5 | 5 | |
| 乙 | 4 | 3 | 3 | 4 | 3 | 5 | 6 | 4 |
（2）求甲种计算器本周销售量的方差．
（3）已知乙种计算器本周销售量的方差为$\frac{8}{7}$，本周哪种计算器的销售量比较稳定？说明理由．
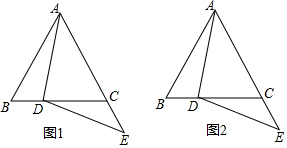在等边△ABC中，点D在BC边上，点E在AC的延长线上，DE=DA（如图1）