题目内容
6．
如图，若∠A=27°，∠B=45°，∠C=38°，则∠DFE等于（ ）| A． | 110° | B． | 115° | C． | 120° | D． | 125° |
分析 根据三角形外角的性质三角形的一个外角等于和它不相邻的两个内角的和可得∠AEB=∠A+∠C=65°，∠DFE=∠B+∠AEC，进而可得答案．
解答 解：∵∠A=27°，∠C=38°，
∴∠AEB=∠A+∠C=65°，
∵∠B=45°，
∴∠DFE=65°+45°=110°，
故选A．
点评 此题主要考查了三角形外角的性质和三角形内角和定理，关键是掌握三角形的一个外角等于和它不相邻的两个内角的和．
练习册系列答案
相关题目
16．若角α、β是直角三角形的两个锐角，则$\frac{sinα}{cosβ}$-tan$\frac{α+β}{2}$的值为（ ）
| A． | 0 | B． | 1 | C． | 1-$\sqrt{2}$ | D． | $\frac{\sqrt{2}}{2}$-1 |
如图，已知等腰直角三角ACB的边AC=BC=a，等腰直角三角形BED的边BE=DE=b
14．下列运算正确的是（ ）
| A． | 3x+3y=6xy | B． | -y2-y2=0 | C． | 3（x+8）=3x+8 | D． | -（6x+2y）=-6x-2y |
1．
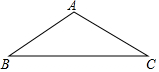如图，某厂房人字架屋顶的上弦AB=AC=10米，∠β=α，则该屋顶的跨度BC为（ ）
如图，某厂房人字架屋顶的上弦AB=AC=10米，∠β=α，则该屋顶的跨度BC为（ ）| A． | 10sinα米 | B． | 10cosα米 | C． | 20sinα米 | D． | 20cosα米 |
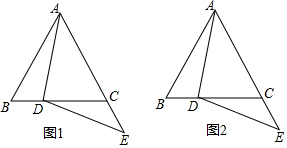在等边△ABC中，点D在BC边上，点E在AC的延长线上，DE=DA（如图1）