题目内容
7.(1)计算:($\sqrt{2}$-3)0-$\sqrt{9}$-(-1)2013-|-2|+(-$\frac{1}{3}$)-2(2)化简求值:($\frac{x-1}{x}$-$\frac{x-2}{x+1}$)÷$\frac{2{x}^{2}-x}{{x}^{2}+2x+1}$,其中x满足x2-x-1=0
(3)解方程:$\frac{2}{{x}^{2}-4}$-$\frac{x}{2-x}$=1.
分析 (1)原式第一项利用零指数幂法则计算,第二项利用算术平方根定义计算,第三项利用乘方的意义化简,第四项利用绝对值的代数意义化简,最后一项利用负整数指数幂法则计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把已知等式变形后代入计算即可求出值;
(3)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=1-3+1-2+9=6;
(2)原式=$\frac{(x+1)(x-1)-x(x-2)}{x(x+1)}$•$\frac{(x+1)^{2}}{x(2x-1)}$=$\frac{2x-1}{x(x+1)}$•$\frac{(x+1)^{2}}{x(2x-1)}$=$\frac{x+1}{{x}^{2}}$,
由x2-x-1=0,得到x2=x+1,
则原式=1;
(3)去分母得:2+x(x+2)=x2-4,
解得:x=-3,
经检验x=-3是分式方程的解.
点评 此题考查了分式的化简求值,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.已知四边形ABCD的四条边分别是a、b、c、d.其中a、c是对边,且a2+b2+c2+d2=2ac+2bd,则四边形一定是( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
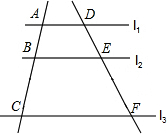 如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F.设AB=3,BC=5,DE=4,则EF=$\frac{20}{3}$.
如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F.设AB=3,BC=5,DE=4,则EF=$\frac{20}{3}$.