题目内容
16.观察下列一组图形,其中图1中共有6个小黑点,图2中共有16个小黑点,图3中共有31个小黑点,…,按此规律,图5中小黑点的个数是( )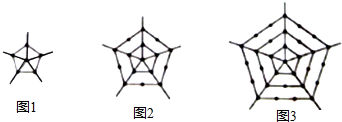
| A. | 46 | B. | 51 | C. | 61 | D. | 76 |
分析 第1个图形小黑点的个数:5×1+1=6;第2个图形小黑点的个数:5×(1+2)+1=16;第3个图形小黑点的个数:5×(1+2+3)+1=31;找出规律即可得到图5中小黑点的个数.
解答 解:由图形1、2、3可以看出,
第1个图形小黑点的个数:5×1+1=6;
第2个图形小黑点的个数:5×(1+2)+1=16;
第3个图形小黑点的个数:5×(1+2+3)+1=31;
所以第5个图形小黑点的个数:5×(1+2+3+4+5)+1=76.
故选:D.
点评 本题考查了探索图形规律问题,解决此类问题的关键是由图形到算式,采用特殊到一般的数学思想方法,归纳出一般规律.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
6.若a=-0.32,b=-3-2,$c={({-\frac{1}{3}})^{-2}}$;$d={({-\frac{1}{3}})^0}$,则它们的大小关系是( )
| A. | a<b<c<d | B. | b<a<d<c | C. | a<d<c<b | D. | c<a<d<b |
11.若分式$\frac{x-2}{x+1}$的值不为0,则x的值为( )
| A. | -1 | B. | 0 | C. | 2 | D. | 不确定 |
1.若抛物线y=x2-2x+c与x轴的一个交点为(3,0),则下列说法不正确的是( )
| A. | 抛物线开口向上 | |
| B. | 抛物线的对称轴是x=1 | |
| C. | 当x=1时,y的最大值为-4 | |
| D. | 关于x的一元二次方程x2-2x+c的两个根为-1,3 |
5.下列条件中,不能判定四边形是平行四边形的是( )
| A. | 相邻角都互补 | B. | 对角线互相平分 | ||
| C. | 两条对角线相等 | D. | 两组对角分别相等 |
 如图,AD是△ABC的角平分线,∠B=30°,∠BAD=50°,求∠ADC和∠C的度数.
如图,AD是△ABC的角平分线,∠B=30°,∠BAD=50°,求∠ADC和∠C的度数. 已知:如图,四边形ABCD中,AB=CB=40,AD=CD=30.
已知:如图,四边形ABCD中,AB=CB=40,AD=CD=30.