题目内容
17.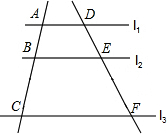 如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F.设AB=3,BC=5,DE=4,则EF=$\frac{20}{3}$.
如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F.设AB=3,BC=5,DE=4,则EF=$\frac{20}{3}$.
分析 根据l1∥l2∥l3,由平行线分线段成比例定理得到成比例线段,代入已知数据计算即可得到答案.
解答 解:∵l1∥l2∥l3,
∴$\frac{AB}{BC}$=$\frac{DE}{EF}$,又AB=3,BC=5,DE=4,
∴EF=$\frac{20}{3}$,
故答案为:$\frac{20}{3}$.
点评 本题考查平行线分线段成比例定理,掌握定理的内容、找准对应关系是解题的关键.

练习册系列答案
相关题目
7.为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆金鱼的比赛,如图所示.

按以上的规律,第n个图形需要的火柴棒m关于n的函数表达式为( )

按以上的规律,第n个图形需要的火柴棒m关于n的函数表达式为( )
| A. | m=8n | B. | m=8+6n | C. | m=4+4n | D. | m=2+6n |
5.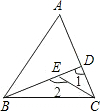 如图所示:D是△ABC中AC边上的一点,E是BD上一点,则对∠1,∠2,∠A之间的关系描述正确的是( )
如图所示:D是△ABC中AC边上的一点,E是BD上一点,则对∠1,∠2,∠A之间的关系描述正确的是( )
 如图所示:D是△ABC中AC边上的一点,E是BD上一点,则对∠1,∠2,∠A之间的关系描述正确的是( )
如图所示:D是△ABC中AC边上的一点,E是BD上一点,则对∠1,∠2,∠A之间的关系描述正确的是( )| A. | ∠A<∠1<∠2 | B. | ∠2<∠1<∠A | C. | ∠1>∠2>∠A | D. | 无法确定 |
2.一次函数y=-5x+3不经过第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
9.若函数y=$\frac{k+1}{x}$的图象在其象限内y随x值的增大而增大,则k的取值范围是( )
| A. | k<1 | B. | k<-1 | C. | k>-1 | D. | k>1 |
6.若a=-0.32,b=-3-2,$c={({-\frac{1}{3}})^{-2}}$;$d={({-\frac{1}{3}})^0}$,则它们的大小关系是( )
| A. | a<b<c<d | B. | b<a<d<c | C. | a<d<c<b | D. | c<a<d<b |
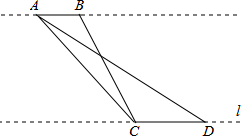 九(1)数学兴趣小组为了测量河对岸的古塔A、B的距离,他们在河这边沿着与AB平行的直线l上取相距20m的C、D两点,测得∠ACB=15°,∠BCD=120°,∠ADC=30°,如图所示,则古塔A、B的距离为$\frac{20\sqrt{3}}{3}$.
九(1)数学兴趣小组为了测量河对岸的古塔A、B的距离,他们在河这边沿着与AB平行的直线l上取相距20m的C、D两点,测得∠ACB=15°,∠BCD=120°,∠ADC=30°,如图所示,则古塔A、B的距离为$\frac{20\sqrt{3}}{3}$.