题目内容
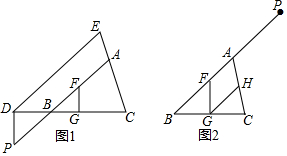
19．
如图，将一副三角板叠放在一起，使直角的顶点重合于点O，AB∥OC，DC与OB交于点E，则∠DEO的度数为75°．
分析 由平行线的性质求出∠AOC=120°，再求出∠BOC=30°，然后根据三角形的外角性质即可得出结论．
解答 解：∵AB∥OC，∠A=60°，
∴∠A+∠AOC=180°，
∴∠AOC=120°，
∴∠BOC=120°-90°=30°，
∴∠DEO=∠C+∠BOC=45°+30°=75°．
故答案为：75°．
点评 本题主要考查了平行线的性质、三角形的外角性质；熟练掌握平行线的性质和三角形的外角性质是解决问题的关键．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
9．
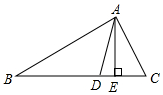如图，在△ABC中，∠ABC=40°，∠ACB=60°，AD是∠BAC的角平分线，AE是BC边上的高，则∠DAE的度数是（ ）
如图，在△ABC中，∠ABC=40°，∠ACB=60°，AD是∠BAC的角平分线，AE是BC边上的高，则∠DAE的度数是（ ）| A． | 10° | B． | 20° | C． | 30° | D． | 40° |
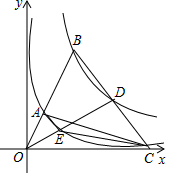如图，点A为双曲线y=$\frac{2}{x}$（x＞0）上一动点，直线OA与双曲线y=$\frac{18}{x}$（x＞0）交于点B，点C（9，0），连CB交双曲线y=$\frac{18}{x}$（x＞0）于点D，连OD交双曲线y=$\frac{2}{x}$（x＞0）于点E，若S△AOC=6S△ACE，则点A坐标为（$\frac{9}{7}$，$\frac{14}{9}$）．
14．下列计算正确的是（ ）
| A． | -5+2=-7 | B． | （-3）2=6 | C． | $\sqrt{4}$-$\root{3}{8}$=0 | D． | 5-2x=3x |
