题目内容
10.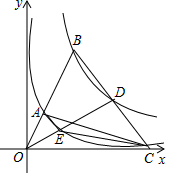 如图,点A为双曲线y=$\frac{2}{x}$(x>0)上一动点,直线OA与双曲线y=$\frac{18}{x}$(x>0)交于点B,点C(9,0),连CB交双曲线y=$\frac{18}{x}$(x>0)于点D,连OD交双曲线y=$\frac{2}{x}$(x>0)于点E,若S△AOC=6S△ACE,则点A坐标为($\frac{9}{7}$,$\frac{14}{9}$).
如图,点A为双曲线y=$\frac{2}{x}$(x>0)上一动点,直线OA与双曲线y=$\frac{18}{x}$(x>0)交于点B,点C(9,0),连CB交双曲线y=$\frac{18}{x}$(x>0)于点D,连OD交双曲线y=$\frac{2}{x}$(x>0)于点E,若S△AOC=6S△ACE,则点A坐标为($\frac{9}{7}$,$\frac{14}{9}$).
分析 设A(a,$\frac{2}{a}$)(a>0),得B(3a,$\frac{6}{a}$),则$\frac{OA}{OB}=\frac{1}{3}$,可得AG∥BC,由OC=9,得OG=3,根据同底边三角形的面积比等于对应高的比可知:即S△ACG=2S△AOG,S△AEC=2S△AOE,
证明得$\frac{AE}{AG}$=$\frac{1}{4}$,由△EMG∽△AHG,得EM=$\frac{3}{2a}$,设MG=3b,GH=4b,列方程组可得结论.
解答 解:设A(a,$\frac{2}{a}$)(a>0),
设直线OA的解析式为:y=kx(k≠0),
$\frac{2}{a}$=ak,
k=$\frac{2}{{a}^{2}}$,
∴直线OA的解析式为:y=$\frac{2}{{a}^{2}}$x,
则$\left\{\begin{array}{l}{y=\frac{2}{{a}^{2}}x}\\{y=\frac{18}{x}}\end{array}\right.$,
$\frac{18}{x}$=$\frac{2x}{{a}^{2}}$,
x=±3a,
∵B在第一象限,
∴B(3a,$\frac{6}{a}$),
∴$\frac{OA}{OB}=\frac{1}{3}$,
延长AE交x轴于G,
同理得:$\frac{OE}{OD}=\frac{OG}{OC}=\frac{1}{3}$,
∴AG∥BC,
∵OC=9,
∴OG=3,
过O作OP⊥AG于P,过C作CQ⊥AG于Q,
∴OP∥CQ,
∴$\frac{OP}{CQ}=\frac{OG}{GC}$=$\frac{3}{6}$=$\frac{1}{2}$,
∴$\frac{{S}_{△ACG}}{{S}_{△AOG}}$=2,即S△ACG=2S△AOG,
同理得:S△AEC=2S△AOE,
∵S△AOC=6S△ACE,
∴3S△AOG=6×2S△AOE,
S△AOG=4S△AOE,
∴$\frac{AE}{AG}$=$\frac{1}{4}$,
过A作AH⊥x轴于H,过E作EM⊥x轴于M,
∴AH∥EH,
∴△EMG∽△AHG,
∴$\frac{EM}{AH}=\frac{EG}{AG}=\frac{MG}{HG}=\frac{3}{4}$,
∴$\frac{EM}{\frac{2}{a}}$=$\frac{3}{4}$,
∴EM=$\frac{3}{2a}$,
设MG=3b,GH=4b,
∴E(3-3b,$\frac{3}{2a}$),
则$\left\{\begin{array}{l}{a+4b=3}\\{(3-3b)•\frac{3}{2a}=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{9}{7}}\\{b=\frac{3}{7}}\end{array}\right.$,
∴A($\frac{9}{7}$,$\frac{14}{9}$).
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法、平行线分线段成比例定理,比较复杂,本题中由反比例函数的关系式得到OA与OB的比是关键.

(1)∠α与∠β互为补角,并且∠β的一半比∠α小30°,求∠α、∠β的度数;
(2)若一辆汽车匀速行驶,有一天途径王家庄、青山、秀水三地的时间如表所示,翠湖在青山、秀水两地之间,距青山60千米,距秀水70千米,王家庄到翠湖的路程有多远?
| 地名 | 时间 |
| 王家庄 | 9:00 |
| 青山 | 12:00 |
| 秀水 | 14:00 |
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{(-2)^{2}}$=-2 | C. | $\sqrt{8}$=2$\sqrt{2}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=2 |
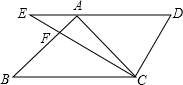 将一副三角板中的两个直角三角板如图放置,使点A在DE上,BC∥DE,其中∠B=∠ACB=45°,∠D=60°,则∠ACE的度数为( )
将一副三角板中的两个直角三角板如图放置,使点A在DE上,BC∥DE,其中∠B=∠ACB=45°,∠D=60°,则∠ACE的度数为( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
 如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,DC与OB交于点E,则∠DEO的度数为75°.
如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,DC与OB交于点E,则∠DEO的度数为75°.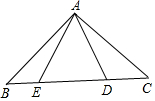 如图,在△ABC中,∠BAC=90°,AB=AC,点D、E在BC上,且∠DAE=45°,若DE=$\sqrt{15}$,CD=$\sqrt{11}$,则BE=2.
如图,在△ABC中,∠BAC=90°,AB=AC,点D、E在BC上,且∠DAE=45°,若DE=$\sqrt{15}$,CD=$\sqrt{11}$,则BE=2.