题目内容
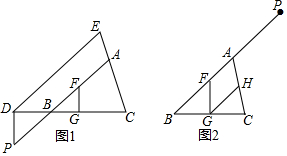
4.已知:三角形ABC中,点F,G分别在线段AB,BC上,FG⊥BC于G,点P在直线AB上运动,PD⊥BC交直线BC于D,过点D作DE∥PA,交直线AC于E.(1)如图1,当点P在线段AB的延长线上时,求证:∠BFG+∠PDE=180°;
(2)如图2,当点P在线段BA的延长线上时,将图补充完整,点H在线段AC上,连接GH,若∠FGH+∠PDE=180°,求证:∠GHC=∠DEC;
(3)在(2)的条件下,延长ED至点S,延长BD至点T,若∠PDS:∠SDT=3:2,$\frac{1}{2}$∠GFA+∠BAC=129°,则∠GHC的度数是66°(直接写出结果)
分析 (1)∠根据平行线的性质得到DE∥PA,于是得到∠FBG=∠EDG即可得到结论;
(2)根据平行线的判定和性质即可得到结论;∠GHC=∠DEC;
(3)根据已知条件得到∠PDS=54°,∠SDT=36°,求得∠CDE=36°,根据平行线的性质得到DE∥PA,根据平行线的性质得到∠BFG=∠BPD=54°,即可得到结论.
解答 解:(1)∠BFG=90°-∠FBG,
∠PDE=90°+∠EDG,
又DE∥PA,
∴∠FBG=∠EDG
∴∠BFG+∠PDE=180°;
(2)如图,∵∠FGH=90°-∠HGD,
∠PDE=90°+∠EDG,
又∠FGH+∠PDE=180°,
∴∠HGD=∠EDG,
HG∥DE,
∴∠GHC=∠DEC;
(3)∵∠PDS:∠SDT=3:2,PD⊥BC,
∴∠PDS=54°,∠SDT=36°,
∴∠CDE=36°,
∴∠PDE=126°,
∵DE∥PA,
∴∠BPD=∠PDS=54°,∠DEC=∠BAC,
∵FG⊥BC,PD⊥BC,
∴FG∥PD,
∴∠BFG=∠BPD=54°,
∴$\frac{1}{2}$∠GFA=63°,
∵$\frac{1}{2}$∠GFA+∠BAC=129°,
∴∠BAC=66°,∠DEC=66°,
由(2)知∠GHC=∠DEC,
∴∠GHC=66°,
故答案为:66°.
点评 本题主要考查了三角形的内角和定理,平行线的判定和性质,互为余角、补角的性质,解题的关键是能够利用这些知识进行角的计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.在平面直角坐标系中,有二次函数y=x2的图象向下平移3个单位,所得图象的解析式为( )
| A. | y=(x-3)2 | B. | y=x2+3 | C. | y=(x+3)2 | D. | y=x2-3 |
15.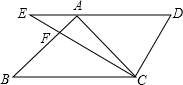 将一副三角板中的两个直角三角板如图放置,使点A在DE上,BC∥DE,其中∠B=∠ACB=45°,∠D=60°,则∠ACE的度数为( )
将一副三角板中的两个直角三角板如图放置,使点A在DE上,BC∥DE,其中∠B=∠ACB=45°,∠D=60°,则∠ACE的度数为( )
 将一副三角板中的两个直角三角板如图放置,使点A在DE上,BC∥DE,其中∠B=∠ACB=45°,∠D=60°,则∠ACE的度数为( )
将一副三角板中的两个直角三角板如图放置,使点A在DE上,BC∥DE,其中∠B=∠ACB=45°,∠D=60°,则∠ACE的度数为( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
9.已知2x2-ax-2=0,给出下列结论:①当x=2时,a+$\frac{1}{a}$=$\frac{10}{3}$;②若a=1时,2x2+$\frac{2}{{x}^{2}}$=6;③若a=2时,x3-4x2+2x=-3,其中正确的是( )
| A. | ①②③ | B. | ①② | C. | ②③ | D. | ①③ |
16.小明掷一枚质地均匀的硬币连续掷了3次,其中2次正面朝上、1次反面朝上的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
13.下列各组数中,数值相等的一组是( )
| A. | 32与23 | B. | (-2)2与-22 | C. | -(-2)与|-2| | D. | ($\frac{2}{3}$)2与$\frac{{2}^{2}}{3}$ |
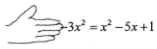 老师在黑板上书写一个正确的演算过程,随后用手掌捂住了一个二次三项式.形式如下:
老师在黑板上书写一个正确的演算过程,随后用手掌捂住了一个二次三项式.形式如下: 如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,DC与OB交于点E,则∠DEO的度数为75°.
如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,DC与OB交于点E,则∠DEO的度数为75°.