题目内容
1.已知在Rt△ABC中,∠C=90°,sinA=$\frac{3}{7}$,BC=4,则AB的长度为( )| A. | $\frac{4}{3}$ | B. | $\frac{7}{4}$ | C. | $\frac{8\sqrt{10}}{3}$ | D. | $\frac{28}{3}$ |
分析 根据正弦函数的定义得出sinA=$\frac{BC}{AB}$,即$\frac{3}{7}$=$\frac{4}{AB}$,即可得出AB的值.
解答 解:∵sinA=$\frac{BC}{AB}$,即$\frac{3}{7}$=$\frac{4}{AB}$,
∴AB=$\frac{28}{3}$,
故选:D.
点评 本题主要考查解直角三角形,熟练掌握正弦函数的定义是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列说法不正确的是( )
| A. | 平行四边形的对边平行且相等 | B. | 平行四边形对角线互相平分 | ||
| C. | 平行四边形是轴对称图形 | D. | 平行四边形是中心对称图形 |
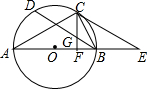 如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.
如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.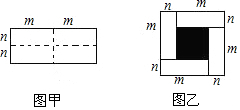 已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.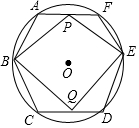 如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,连接PB,QE,PE,BQ.设运动时间为t(s).
如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,连接PB,QE,PE,BQ.设运动时间为t(s).