题目内容
⊙O的半径是2,它的两条弦AB、AC的长分别2
,2
,则∠BAC= °.
| 2 |
| 3 |
考点:垂径定理,特殊角的三角函数值
专题:分类讨论
分析:作OD⊥AB于D,OE⊥AC于E,如图,根据垂径定理得到AD=BD=
,AE=CE=
,在Rt△OAD中,利用余弦定义得cos∠OAD
,所以∠OAD=45°;在Rt△OAE中,由于cos∠OAE=
,所以∠OAD=30°,然后分类讨论:当圆心0在∠BAC内部,则∠BAC=∠OAB+∠OAC;当圆心0在∠BAC外部,则∠BAC=∠OAB-∠OAC.
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
解答:解: 作OD⊥AB于D,OE⊥AC于E,如图,
作OD⊥AB于D,OE⊥AC于E,如图,
∵AB=2
,AC=2
,
∴AD=BD=
,AE=CE=
,
在Rt△OAD中,∵cos∠OAD=
=
,
∴∠OAD=45°;
在Rt△OAE中,∵cos∠OAE=
=
,
∴∠OAD=30°,
当圆心0在∠BAC内部,则∠BAC=∠OAB+∠OAC=45°+30°=75°,
当圆心0在∠BAC外部,则∠BAC=∠OAB-∠OAC=45°-30°=15°.
故答案为15°或75°.
 作OD⊥AB于D,OE⊥AC于E,如图,
作OD⊥AB于D,OE⊥AC于E,如图,∵AB=2
| 2 |
| 3 |
∴AD=BD=
| 2 |
| 3 |
在Rt△OAD中,∵cos∠OAD=
| AD |
| OA |
| ||
| 2 |
∴∠OAD=45°;
在Rt△OAE中,∵cos∠OAE=
| AE |
| AO |
| ||
| 2 |
∴∠OAD=30°,
当圆心0在∠BAC内部,则∠BAC=∠OAB+∠OAC=45°+30°=75°,
当圆心0在∠BAC外部,则∠BAC=∠OAB-∠OAC=45°-30°=15°.
故答案为15°或75°.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.记住特殊角的三角函数值.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
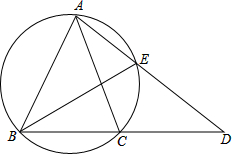 如图,已知E是等腰△ABC外接圆上的点,
如图,已知E是等腰△ABC外接圆上的点,
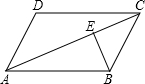 如图,在平行四边形ABCD中,对角线AC=15cm,BE⊥AC于E,且BE=4cm,若AD=6cm,则AD与BC之间的距离为
如图,在平行四边形ABCD中,对角线AC=15cm,BE⊥AC于E,且BE=4cm,若AD=6cm,则AD与BC之间的距离为