题目内容
设圆的半径为rcm，把半径增长到3cm，得到一个大圆，把半径减少2cm，得到一个小圆，问大圆的面积比小圆面积大多少？
考点：列代数式
专题：
分析：先得出大圆和小圆的半径，再得出大圆的面积和小圆面积，从而得出答案．
解答：解：大圆和小圆的半径分别为（r+3）cm，（r-2）cm，
大圆的面积=π（r+3）2，
小圆面积=π（r-2）2，
∴大圆的面积比小圆面积大π（r+3）2-π（r-2）2=π（r+3+r-2）（r+3-r+2）=5π（2r+1）cm．
大圆的面积=π（r+3）2，
小圆面积=π（r-2）2，
∴大圆的面积比小圆面积大π（r+3）2-π（r-2）2=π（r+3+r-2）（r+3-r+2）=5π（2r+1）cm．
点评：本题考查了列代数式，要熟悉圆的面积的计算公式．
练习册系列答案
相关题目
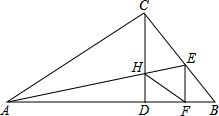如图，在Rt△ABC中，∠ACB=90°，过C作AB的垂线CD交AB于D，过A作∠BAC的角平分线AE交BC于E，AE交CO于H，过E作EF⊥AB交AB于F，连接HF，求证：四边形CHFE为菱形．如图，函数y1=ax+b与y2=bx+a正确的图象为（ ）
A、 |
B、 |
C、 |
D、 |
如图，矩形ABCD与圆心在AB上的⊙O交于点G、B、F、E．已知GB=10cm，AG=2cm，DE=3cm，求EF的长．
如图，
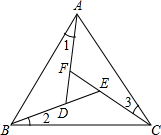如图，已知在△ABC中，∠BAC=∠ACB=∠CBA，∠1=∠2=∠3．