Question

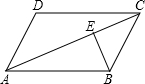如图，在平行四边形ABCD中，对角线AC=15cm，BE⊥AC于E，且BE=4cm，若AD=6cm，则AD与BC之间的距离为

 

cm．

Answer 1

考点：平行四边形的性质

专题：

分析：利用等积法，设AD与BC之间的距离为h，由条件可知?ABCD的面积是△ABC的面积的2倍，可求得?ABCD的面积，再S_{四边形ABCD}=AD•h，可求得h．

解答：解：
∵四边形ABCD为平行四边形，
∴AB=CD，AD=BC，
在△ABC和△CDA中

AB=CD AD=BC AC=CA

∴△ABC≌△CDA（SSS），
∵BE⊥AC，AC=15cm，BE=4cm，
∴S_△ABC=

1

2

AC•BE=

1

2

×15×4=30（cm²），
∴S_{四边形ABCD}=2S_△ABC=60cm²，
设AD与BC之间的距离为h，
则S_{四边形ABCD}=AD•h=6h，
∴6h=60，
解得h=10cm，
故答案为：10．

点评：本题主要考查平行四边形的性质，由条件得到四边形ABCD的面积是△ABC的面积的2倍是解题的关键，再借助等积法求解使解题事半功倍．